A group of n students sit two exams. Exam one is on history and exam two is on chemistry. Let x_i and y_i denote the ith student's score in the history and chemistry exams, respectively. The following linear regression model is proposed for the relationship between the two exam scores:

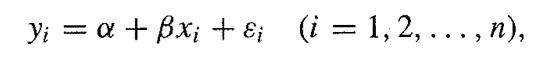 where ε_i ~ N(O, 1/τ).

Assume that x = (x₁, x₂ , ... , X_n) and y = (y₁, y₂ , ... , Y_n) and that a, β and τ are unknown parameters to be estimated.

Describe a reversible jump MCMC algorithm including discussion of the acceptance probability, to move between the four competing models: 

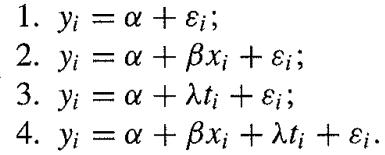
Note that if z is a random variable with probability density function f given by

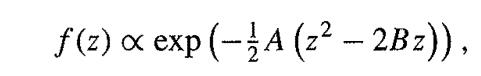
then z ~ N(B, 1/ A) [due to P. Neal].  

Transcribed Image Text:

Yi = a + Bx; + &; (i=1,2,..., n),