Express in your own words the arguments given by Jeffreys (1961, Section 5.2) in favour of a Cauchy distribution

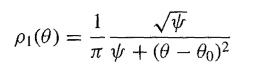
in the problem discussed in the previous question.

Previous question

Lindley (1957) originally discussed his paradox under slightly different assumptions from those made in this book. Follow through the reasoning used in Section 4.5 with P₁ (θ) representing a uniform distribution on the interval (θ₀ - ½ τ, θ₀ + ½τ) to find the corresponding Bayes factor assuming that τ² ≫ ϕ > / n, so that an N(µ, ϕ / n) variable lies in this interval with very high probability. Check that your answers are unlikely to disagree with those found in Section 4.5 under the assumption that P₁ (θ) represents a normal density. 

P(0) = 1 T +(000)