Prove the theorem quoted without proof in Section 2.4. Theorem 2.1. A random sample x = (x,x2,...,xn)

Prove the theorem quoted without proof in Section 2.4.

Transcribed Image Text:

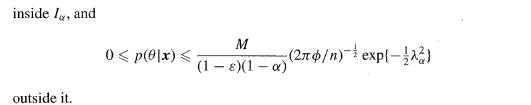
Theorem 2.1. A random sample x = (x₁,x2,...,xn) of size n is taken from N(0, 0) where is known. Suppose that there exist positive constants a, e, M and c depending on x (small values of a and are of interest), such that in the interval la defined by -da√(0/n) ≤0 ≤ x + √(/n), where 2Φ(-λα) = α the prior density of lies between c(1-e) and c(1 + ) and outside I, it is bounded by Mc. Then the posterior density p(x) satisfies (1-8) (1+8)(1-a) + Ma