Show that in any experiment E in which there is a possible value y for the random variable X such that PX(y) = 0, then

Show that in any experiment E in which there is a possible value y for the random variable X̃ such that PX̃(y∣θ) = 0, then if z is any other possible value of X̃, the statistic t = t(x) defined by 

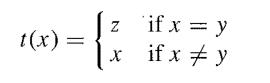
is sufficient for θ given X̃. Hence, show that if x is a continuous random variable, then a naïve application of the weak sufficiency principle as defined in Section 7.1 would result in Ev{E, y, θ} = Ev{E, z, θ} for any two possible values y and z of X̃.

>= { z if x = y x if x = y t(x) =