Suppose that the prior distribution p(,) for the parameters , and of a Cauchy distribution is uniform in and , and that two

Suppose that the prior distribution p(µ,σ) for the parameters µ, and σ of a Cauchy distribution

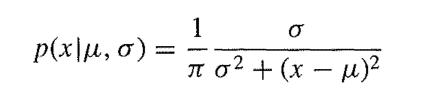
is uniform in µ and σ, and that two observations x₁ = 2 and x₂ = 6 are available from this distribution. Calculate the value of the posterior density p(µ, σlx) (ignoring the factor 1/π²) to two decimal places for µ, = 0, 2, 4, 6, 8 and σ = 1, 2, 3, 4, 5. Use Simpson's rule to approximate the posterior marginal density of µ, and hence go on to find an approximation to the posterior probability that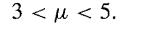 

p(x\u,6) = 1 2 + (x - )2