Suppose that x ~ C(0, 1) has a Cauchy distribution. It is easily shown that = P(x > 2) = tan -1 ()/ =

Suppose that x ~ C(0, 1) has a Cauchy distribution. It is easily shown that η = P(x > 2) = tan^-1(½)/π = 0.147 583 6, but we will consider Monte Carlo methods of evaluating this probability.

(a) Show that if k is the number of values taken from a random sample of size n with a Cauchy distribution, then k / n is an estimate with variance 0.125 802 7 . 

(b) Let p(x) = 2/x², so that  ∫_x^∞ p (ξ) dξ 2/x. Show that if x ~ U(0, 1) is uniformly distributed over the unit interval then y = 2/x has the density p(x) and that all values of y satisfy y ≥ 2 and hence that

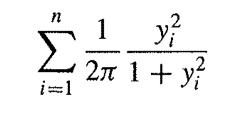
gives an estimate of η by importance sampling.

(c) Deduce that if x₁, x₂ , ... , X_n are independent U(0, 1) variates then

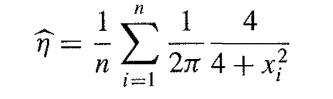
gives an estimate of η.

( d) Check that η̂ is an unbiased estimate of η and show that

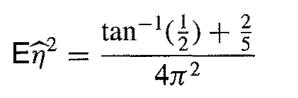
and deduce that 

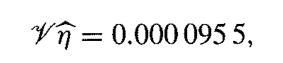
so that this estimator has a notably smaller variance than the estimate considered in (a).

n 1 y 21 + y - 2