Exercise 12.12 Consider a Brownian motion {X(t)} with drift and diffusion coefficient defined on the interval [0, a], where the boundaries 0 and

Exercise 12.12 Consider a Brownian motion {X(t)} with drift μ and diffusion coefficient σ defined on the interval [0, a], where the boundaries 0 and a > 0 are absorbing. Using the transformation (12.15) and the result (10.19)

with N = a/Δx, show that the transition density function a(x, y, t) of the Brownian motion is given by

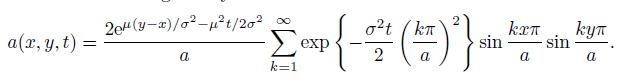
20(y-x)/02-21/20 a(x, y, t) = exp a k=1 -{ (7))}. o2t (km sin 2 kx sin a a