Exercise 3.1 (Discrete Convolution) Let X and Y be non-negative, discrete random variables with probability distributions p^Xi

= P{X = i} and p^Yi

= P{Y = i}, i = 0, 1, 2, . . . , respectively, and suppose that they are independent.

Prove that

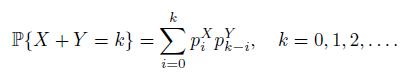
Using this formula, prove that if X ∼ B(n, p), Y ∼ Be(p) and they are independent, then X + Y ∼ B(n + 1, p).

Px-i, k = 0, 1, 2,.... k XY P{X+Y=k} = PP- i=0