Exercise 3.9 (Convolution Formula) Let X and Y be continuous random variables with density functions fX(x) and fY (x), respectively, and suppose that they are independent. Prove that the density function of X + Y is given by

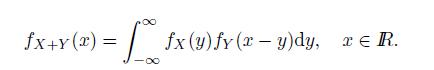
Using this, prove that if X ∼ N(μX, σ2X), Y ∼ N(μY , σ2Y ) and they are independent, then X + Y ∼ N(μX + μY , σ2X + σ2Y ). Also, prove (3.25) by an induction on k.

fx+y(x) = =L fx (y)fy (xy)dy, rR.