Exercise 5.7 For random variable X, suppose that the moment generating function m(t) = E[etX] exists for any t > 0. Let (t) = logm(t),

Exercise 5.7 For random variable X, suppose that the moment generating function m(t) = E[e−tX] exists for any t > 0. Let ϕ(t) = logm(t), called the cumulant generating function. Prove the following.

(1) ϕ(t) is decreasing in t if and only if

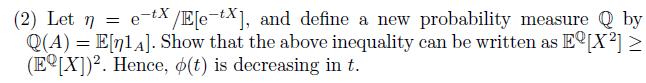
E[XetX]E[etX] (E[XeX]).