Hypergeometric Distribution If we sample from a small finite population without replacement, the binomial distribution should not be used because the events are not independent.

If sampling is done without replacement and the outcomes belong to one of two types, we can use the hypergeometric distribution. If a population has A objects of one type, while the remaining B objects are of the other type, and if n objects are sampled without replacement, then the probability of getting x objects of type A and n - x objects of type B is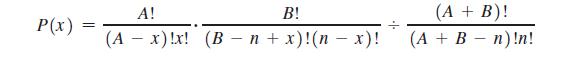

In a medical research project, there are 20 subjects available and 4 of them are infected with HIV, while the other 16 are not infected. If 8 of the subjects are randomly selected without replacement, what is the probability that 3 of the subjects are infected with HIV, while the other 5 are not infected? What is the probability if the sampling is done with replacement?

P(x) = A! B! (A x)!x! (B n + x)!(n - x)! (A + B)! (A + B - n)!n!