Question: Consider testing H 0 : 1 = 0 versus Ha: 1 0. Figure 14.11 tells us that t = 14.44 and that

Consider testing H₀: β₁ = 0 versus Ha: β₁ ≠ 0. Figure 14.11 tells us that t = 14.44 and that the related p-value is less than .001. Assuming that the bivariate normal probability distribution assumption holds, test H₀: p = 0 versus H_a: p ≠ 0 by setting a equal to .05, .01, and .001. What do you conclude about how x and y are related?

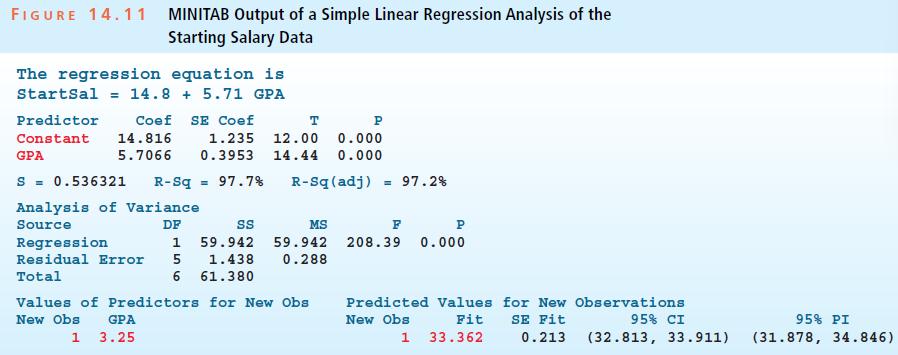
FIGURE 14.11 MINITAB Output of a Simple Linear Regression Analysis of the

FIGURE 14.11 MINITAB Output of a Simple Linear Regression Analysis of the Starting Salary Data The regression equation is Startsal = 14.8+5.71 GPA Coef SE Coef T P 1.235 12.00 0.000 5.7066 0.3953 14.44 0.000 Predictor Constant 14.816 GPA S = 0.536321 R-Sq 97.7% R-Sq(adj) = 97.2% Analysis of Variance Source DF SS MS 1 59.942 59.942 1.438 0.288 6 61.380 Regression Residual Error 5 Total Values of Predictors for New Obs New Obs 1 GPA 3.25 P F 208.39 0.000 Predicted Values New Obs Fit 1 33.362 for New Observations SE Fit 95% CI 0.213 (32.813, 33.911) 95% PI (31.878, 34.846)

Step by Step Solution

★★★★★

3.56 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

In this context you are considering the pvalue from a simple linear regression analysis that tests t... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Business Statistics A First Course Questions!

Consider testing H0: 1 = 0 versus Ha: 1 = 0. Figure tells us that t = 30.5802 and that the related p-value is less than .001. Assuming that the bivariate normal probability distribution assumption...

Consider testing H0: 1 = 0 versus Ha: 1 0. Figure tells us that t = 7.3277 and that the related p-value is .0003. Assuming that the bivariate normal probability distribution assumption holds, test...

A common application of the sign test deals with analyzing consumer preferences. For instance, suppose that a blind taste test is administered to nine randomly selected convenience store customers....

Find the appropriate rejection regions for the large-sample test statisticz in these cases. (Round your answers to two decimal places. It the test is one-tailed, enter NONE for the unused region.)...

Business Statistics assignment 3 Question1 For a parameter whose value is unknown, belief or claim for that parameter is classified as_________. Select one: a.parameter claim testing b.hypothesis...

STAT\t501\t-\tHomework\t6\t-\tSpring\t2017\t-\tDue\tFeb\t19 Instructions:\tUse\tWord\tto\ttype\tyour\tanswers\twithin\tthis\tdocument.\tThen,\tsave\tand\tupload...

summarize the main idea of each article, discuss issues being highlighted briefly, give opinion pertaining the coverage of each article and provide recommendations for each issue in the article....

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

Americas Company has a plant capacity of 100,000 units per year, but its bud get for this year indicates that only 60,000 units will be produced and sold. The entire budget for this year follows. 1....

Assume expected returns and standard deviations as follows: The correlation coefficient, p, is +.15 EG&G Retum (%) Standard deviation (% Covariance (%) 25 30 1 12.5 23 ) 25

What is the maximum frame size supported by Ethernet networks? a . 1 5 0 0 bytes * b . 2 0 0 0 bytes c . 4 0 9 6 bytes d . 8 1 9 2 bytes

14.1* Prove expression (14.2). with the associated defirution of a,, c,. (Recall that o2 and T? are assumed known. Hint: first derive the distributions of y I y and 8, I p, y and then integrate out p...

In order to gain additional information about respondents, some marketing researchers have used ultraviolet ink to precode questionnaires that promise confidentiality to respondents. Of 205 randomly...

When a store uses electronic article surveillance (EAS) to combat shoplifting, it places a small sensor on each item of merchandise. When an item is legitimately purchased, the sales clerk is...

A department store will place a sale item in a special display for a one-day sale. Previous experience suggests that 20 percent of all customers who pass such a special display will purchase the...

Sheffield Frame Camera Shop uses the lower-of-cost-or-net realizable value basis for its inventory. The following data are available at December 31 . What amount should be reported for inventory on...

Dividends on Preferred and Common Stock Pecan Theatre Inc. owns and operates movie theaters throughout Florida and Georgia. Pecan Theatre has declared the following annual dividends over a six-year...

Krall Company recently had a computer malfunction and lost a portion of its accounting records. The company has reconstructed some of its financial performance measurements including components of...