Find the average value of the function over the given solid. The average value of a continuous function (x, y, z) over a solid region

Find the average value of the function over the given solid. The average value of a continuous function ƒ(x, y, z) over a solid region Q is

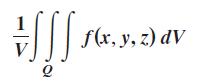
where V is the volume of the solid region Q.

ƒ(x, y, z) = x + y + z over the tetrahedron in the first octant
with vertices (0, 0, 0), (2, 0, 0), (0, 2, 0), and (0, 0, 2)

#fff f(x, y, z) dv