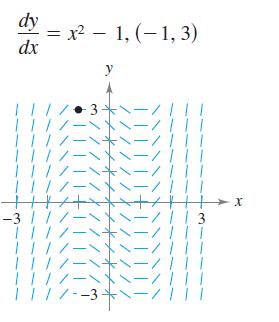
Question: In Exercises a differential equation, a point, and a slope field are given. A slope field (or direction field) consists of line segments with slopes
In Exercises a differential equation, a point, and a slope field are given. A slope field (or direction field) consists of line segments with slopes given by the differential equation. These line segments give a visual perspective of the slopes of the solutions of the differential equation.
(a) Sketch two approximate solutions of the
differential equation on the slope field, one of which passes
through the indicated point.
(b) Use integration to find the
particular solution of the differential equation and use a
graphing utility to graph the solution. Compare the result with
the sketches in part (a).
dy =x-1, (-1, 3) dx 1/ | | || / / 11 //- 11/ + -31 y 3*\-/1 /-/||| -7/111 11 11 //- 11 //--3 -/111 -2111 ++ -/13 X
Step by Step Solution
3.26 Rating (167 Votes )
There are 3 Steps involved in it
a ... View full answer

Get step-by-step solutions from verified subject matter experts


