Question: In Exercises find a geometric power series for the function, centered at 0 (a) By the technique shown in Examples 1 (b) By long division
In Exercises find a geometric power series for the function, centered at 0
(a) By the technique shown in Examples 1
(b) By long division
Data from in Examples 1

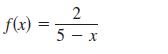
Long Division 2 x + xx+. 2 + x) 4 4 + 2x -2x -2x - x x x + x EXAMPLE 1 Finding a Geometric Power Series Centered at 0 Find a power series for f(x): 4 x + 2' Solution Writing f(x) in the form a/(1-r) produces 4 2 1-(-x/2) 2 + x which implies that a = 2 and r = = X So, the power series for f(x) is 4 x + 2 = = 00 n=0 00 ar" = 11 a A=0 = 2(1 This power series converges when centered at 0. . ) which implies that the interval of convergence is (-2,2). Another way to determine a power series for a rational function such as the one in Example 1 is to use long division. For instance, by dividing 2 + x into 4, you obtain the result shown at the left.
Step by Step Solution
3.48 Rating (158 Votes )
There are 3 Steps involved in it
a b 511245 X ... View full answer

Get step-by-step solutions from verified subject matter experts


