Question: Let be a positive, continuous, and decreasing function for x 1, such that a n = (n). Prove that if the series converges

Let ƒ be a positive, continuous, and decreasing
function for x ≥ 1, such that an = ƒ(n). Prove that if the series

n=1

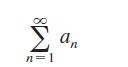
converges to S, then the remainder RN S - SN is bounded by

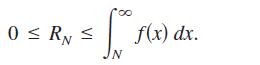
n=1

Step by Step Solution

★★★★★

3.55 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

1 SN f1 a f2a 2 fN 1 an1 f... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 10th Edition Questions!

Q:

Let be a positive number. A differential equation of the form dy/dt = ky1+c where is a positive constant, is called a doomsday equation because the exponent in the expression ky1+c is larger than...

Q:

Let x be a positive continuous random variable. Prove that EX = P(X x) dx.

Q:

Let f, g be bounded on [a, b]. a) Prove that and b) Prove that and for a (U)| f(x)dx=(U) | f(x)dx+(U)| f(x)dx so

Q:

In Exercises use the result of Exercise 53 to approximate the sum of the convergent series using the indicated number of terms. Include an estimate of the maximum error for your approximation. Data...

Q:

In Exercises use the result of Exercise 53 to approximate the sum of the convergent series using the indicated number of terms. Include an estimate of the maximum error for your approximation. Data...

Q:

In Exercises use the result of Exercise 53 to approximate the sum of the convergent series using the indicated number of terms. Include an estimate of the maximum error for your approximation. Data...

Q:

In Exercises use the result of Exercise 53 to approximate the sum of the convergent series using the indicated number of terms. Include an estimate of the maximum error for your approximation. Data...

Q:

In Exercises use the result of Exercise 53 to approximate the sum of the convergent series using the indicated number of terms. Include an estimate of the maximum error for your approximation. Data...

Q:

In Exercises use the result of Exercise 53 to approximate the sum of the convergent series using the indicated number of terms. Include an estimate of the maximum error for your approximation. Data...

Q:

In Exercises use the result of Exercise 53 to find N such that R N 0.001 for the convergent series. Data from in Exercise 53 Let be a positive, continuous, and decreasing function for x 1, such...

Q:

A gas mixture containing 85.0 mole% N2 and the balance n-hexane flows through a pipe at a rate of 100.0m 3 fh, the pressure is 2.00 atm absolute and the temperature is 100C. (a) What is the molar...

Q:

Performance of an electric dust collector (see Fig. 2C.1) 5 (a) A dust precipitator consists of a pair of oppositely charged plates between which dust-laden gases flow. It is desired to establish a...

Q:

Displaying Distributions with Graphs

Q:

Briefly explain different tools for concurrent engineering.AppendixLO1

Q:

In problem, the function f is one-to-one. Find the inverse of each function and check your answer. f(x) = 1

Q:

To get $600 after 2 years at4%compounded quarterly In problem, find the principal needed now to get each amount; that is, find the present value.

Q:

In problem, the graph of a function f is given. Use the horizontal-line test to determine whether f is one-to-one. y. 3 x -3 -3

Q:

09.03-PR003 Hyundai USA has numerous robotic welders as well as robotic checkers with vision. One underbody robotic welder was installed and is increasing productivity by 2.5% in one area. The result...

Q:

1. Stock in Blue Sky Inc. is currently priced at $28 per share. A call option with a $35 strike and 60 days to maturity is quoted at $1.22. Compare the percentage gains and losses for both options...

Q:

open answer In your opinion, what the biggest Pro of debt financing and Con of debt financing? For the toolbar, press ALT+F10 (PC) or ALT+FN+F10 (Mac)