Let f be a nonnegative function such that ' is continuous over the interval [a, b]. Let S be the surface of revolution formed by

Let f be a nonnegative function such that ƒ'
is continuous over the interval [a, b]. Let S be the surface of
revolution formed by revolving the graph of ƒ, where
a ≤ x ≤ b, about the x-axis. Let x = u, y = ƒ(u) cos v, and
z = ƒ(u) sin v, where a ≤ u ≤ b and 0 ≤ v ≤ 2π. Then,
S is represented parametrically by r(u, v) = ui + ƒ(u) cos vj
+ ƒ(u) sin vk. Show that the following formulas are equivalent.

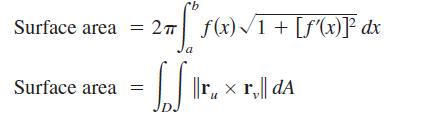
Surface area = Surface area 2 f(x)1 + ['(x)} dx 1 SS. ||r x r|| DA