Let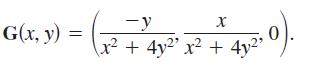

Prove or disprove that there is a a vector-valued function F(x, y, z) = (M(x, y, z), N(x, y, z), P(x, y, z)) with the following properties:

(i) M, N, P have continuous partial derivatives for all
(x, y, z) ≠ (0, 0, 0);

(ii) Curl F = 0 for all (x, y, z) ≠ (0, 0, 0);

(iii) F(x, y, 0) = G(x, y).

G(x, y) = 2. 0). -y X x + 4y x + 4y