Question: Prove the following Extended Mean Value Theorem. If and ' are continuous on the closed interval [a, b], and if exists in the

Prove the following Extended Mean Value Theorem. If ƒ and ƒ' are continuous on the closed interval [a, b], and if ƒ" exists in the open interval
(a, b), then there exists a number c in (a, b) such that

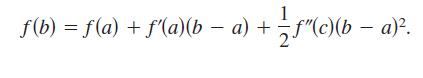
(b) = f(a) + f'(a)(b a) + (c)(b a). - -

(b) = f(a) + f'(a)(b a) + (c)(b a). - -

Step by Step Solution

★★★★★

3.40 Rating (162 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

b a ab a ba Define Fx fx fa fax a kx a Fa 0 Fb fb a ab a kb a 0 F is continu... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 10th Edition Questions!

Q:

ingness to fil out me 10. On your last exam, most students earned 75% of the available points. The ease with which you can now com- pare your own performance is a clear advantage of using a. words to...

Q:

Proof (a) Let 1 (x) and 2 (x) be continuous on the closed interval [a, b]. If 1 (a) 2 (b), prove that there exists c between a and b such that 1 (c) = 2 (c). (b) Show that...

Q:

In Theorem 3.37, prove that if B = A, then PGx = 0 for every x in Z k 2 . (Throughout this proof we denote by ai the ith column of a matrix A.) With P and G as in the statement of the theorem, assume...

Q:

THEOREM 4.4 Mean Value Theorem If f is continuous on the closed interval [a, b] and differentiable on (a, b), then there is at least one point c in (a, b) such that f (b) - f(a) = f' (c). b - a 3....

Q:

The height of a ball t seconds after it is thrown upward from a height of 7 feet and with an initial velocity of 48 feet per second is f(t) = -15t2 + 4st + 7. (a) Verify that f(1) = f(2). HI) = m w...

Q:

In Exercises determine whether the Mean Value Theorem can be applied to on the closed interval [a, b]. If the Mean Value Theorem can be applied, find all values of c in the open interval (a, b) such...

Q:

In Exercises detrmine whether the Mean Value Theorem can be applied to on the closed interval [a, b]. If the Mean Value Theorem can be applied, find all values of c in the open interval (a, b) such...

Q:

In Exercises determine whether the Mean Value Theorem can be applied to on the closed interval [a, b]. If the Mean Value Theorem can be applied, find all values of c in the open interval (a, b) such...

Q:

In Exercises determine whether the Mean Value Theorem can be applied to on the closed interval [a, b]. If the Mean Value Theorem can be applied, find all values of c in the open interval (a, b) such...

Q:

In Exercises determine whether the Mean Value Theorem can be applied to on the closed interval [a, b]. If the Mean Value Theorem can be applied, find all values of c in the open interval (a, b) such...

Q:

In figure shown, determine the minimum weight of block B that will keep it at rest while a force P starts block A up the inclined surface of B. The weight of A is 100 kN and the angle of friction for...

Q:

A random variable X has a Pareto distribution if and only if its probability density is given by Where α > 0. Show that µ'r exists only if r for x >1 elsewhere

Q:

Evelyn has rental income of $ 4 2 , 0 0 0 and passive income of $ 1 4 , 0 0 0 . She also has $ 1 2 6 , 0 0 0 of losses from a real estate rental activity in which whe actively participates. Evelyn's...

Q:

Mary Parker owns Parkers SCUBA Shop in Bathurst. (In your Study Guide with Working Papers, balances as of April 1 are provided for the accounts receivable and general ledger accounts.) In Marys...

Q:

Pollution that increases firm costs - Barney's Solution: Consider the same situation as the one described in exercise 21.9. A: Assume again that the only impact of pollution is that it increases firm...

Q:

Pollution that increases firm costs-Policy Solutions: This exercise continues to build on exercises 21.9 and 21.10. Assume the same basic setup of firms located around a lake producing pollution that...

Q:

Social Norms and Private Actions: When asked to explain our actions, we sometimes simply respond by saying it was the right thing to do. The concept of the right thing to do is one that is often...

Q:

You estimate that by the time you retire in 35 years, you will have accumulated savings of $3.4 million. a. If the interest rate is 10.5% and you live 15 years after tetirement, what annual level of...

Q:

Question 31 (5 points) A company is about to do a seasoned offering and has been offered two alternative choices to raise the funds: a) The investment dealer will underwrite an issue of one million...

Q:

You are looking to invest in one of three stocks. All other things being equal, Stock A has high expected earnings growth, stock B has only modest expected earnings growth, and stock C is expected to...