Recall that the graph of a function y = (x) is symmetric with respect to the origin if, whenever (x, y) is a point on

Recall that the graph of a function y = ƒ(x) is
symmetric with respect to the origin if, whenever (x, y) is a
point on the graph, (-x, -y) is also a point on the graph. The
graph of the function y = ƒ(x) is symmetric with respect to
the point (a, b) if, whenever (a - x, b - y) is a point on the
graph, (a + x, b + y) is also a point on the graph, as shown in
the figure.

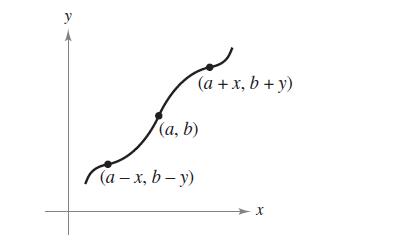
(a) Sketch the graph of y = sin x on the interval [0, 2π]. Write
a short paragraph explaining how the symmetry of the graph
with respect to the point (π, 0) allows you to conclude that

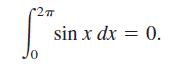
(b) Sketch the graph of y = sin x + 2 on the interval [0, 2π]. Use the symmetry of the graph with respect to the point (π, 2) to evaluate the integral

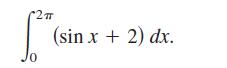
(c) Sketch the graph of y = arccos x on the interval [-1, 1]. Use the symmetry of the graph to evaluate the integral

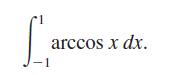
(d) Evaluate the integral

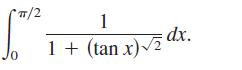
y ((a+5,6+3) (a + x, b + y) (a, b) (a-x, b-y) X