Suppose and g are non-constant, differentiable, real-valued functions defined on (-, ). Furthermore, suppose that for each pair of real numbers x and y,

Suppose ƒ and g are non-constant, differentiable, real-valued
functions defined on (-∞, ∞). Furthermore, suppose that
for each pair of real numbers x and y,

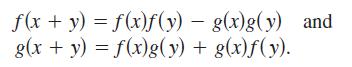
f(x + y) = f(x)f(y) - g(x)g(y) and g(x + y) = f(x)g(y) + g(x)f(y).