(a) Show that any point on x 2 + y 2 = z 2 can be written in the form (z cos , z sin

(a) Show that any point on x² + y² = z² can be written in the form (z cos θ, z sin θ, z) for some θ.
(b) Use this to find a parametrization of Viviani’s curve (Exercise 31) with θ as the parameter.

Data From Exercise 31

C is the intersection of the surfaces (Figure 12)

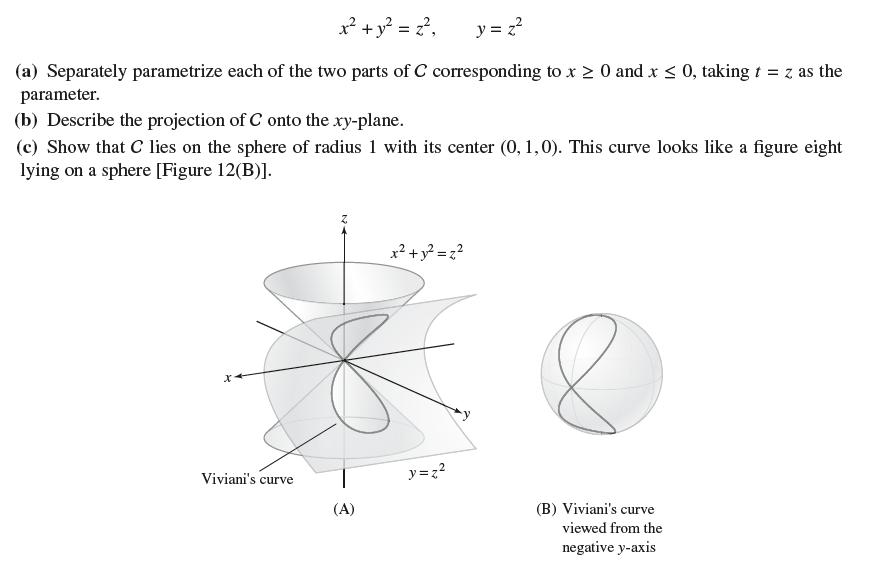
x + y = z, y = z (a) Separately parametrize each of the two parts of C corresponding to x 0 and x 0, taking t = z as the parameter. (b) Describe the projection of C onto the xy-plane. (c) Show that C lies on the sphere of radius 1 with its center (0, 1,0). This curve looks like a figure eight lying on a sphere [Figure 12(B)]. Viviani's curve (A) x + y = z y=z 8 (B) Viviani's curve viewed from the negative y-axis