Continuing with the previous exercise, let tank 2 be another tank filled with V 2 gallons of

Question:

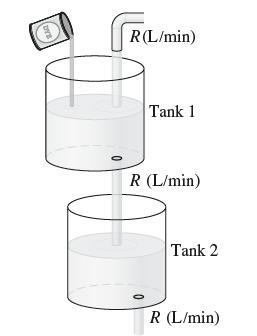
Continuing with the previous exercise, let tank 2 be another tank filled with V₂ gallons of water. Assume that the dye solution from tank 1 empties into tank 2 as in Figure 5, mixes instantaneously, and leaves tank 2 at the same rate R. Let c2(t) be the dye concentration in tank 2 at time t.

3 R (L/min) Tank 1 R (L/min) Tank 2 R (L/min)

(a) Explain why c₂ satisfies the differential equation

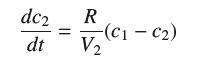
dc2 dt R -(C - C) V

(b) Use the solution to Exercise 43 to solve for c₂(t) if V₁ = 300, V₂ = 200, R = 50, and c₀ = 10.

Data From Exercise 43

Tank 1 in Figure 5 is filled with V₁liters of water containing blue dye at an initial concentration of c₀g/L. Water flows into the tank at a rate of R L/min, is mixed instantaneously with the dye solution, and flows out through the bottom at the same rate R. Let c₁(t) be the dye concentration in the tank at time t.

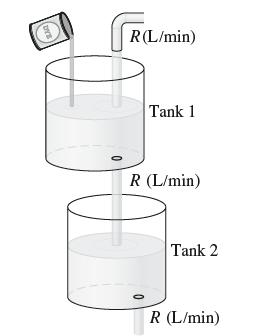
3 R (L/min) Tank 1 R (L/min) Tank 2 R (L/min)