Define P n (x) by Use the reduction formula in Exercise 64 to prove that P n (x) x n nP n1 (x) Use this recursion relation to find P n (x) for n 1, 2, 3, 4 P 0 (x) 1 Data From Exercise 64 xe dx P xe dx Pn(x) et C

Question: Define P n (x) by Use the reduction formula in Exercise 64 to prove that P n (x) = x n nP n1 (x).

Define P_n(x) by

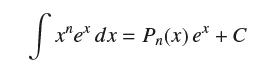
[xe dx = P xe* dx= Pn(x) et + C

Use the reduction formula in Exercise 64 to prove that P_n(x) = xⁿ − nP_n−1(x). Use this recursion relation to find P_n(x) for n = 1, 2, 3, 4. P₀(x) = 1.

Data From Exercise 64

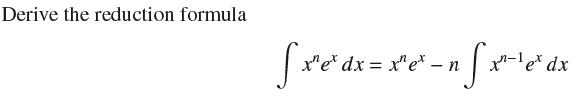
[xe dx = P xe* dx= Pn(x) et + C

Step by Step Solution

★★★★★

3.54 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Data From Exercise 64 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

(a) Use the reduction formula in Example 6 to show that Where n ¥ 2 is an integer (b) Use part (a) to evaluate in X dr an in X dX

The following additional information is available for the Dr. Ivan and Irene Incisor family. The Incisors own a rental beach house in Hawaii. The beach house was rented for the full year during 2012...

854 CHAPTER 15 DIFFERENTIATION IN SEVERAL VARIABLES 9. 20. Jessica and I at 2 oh ; h (x , y ) = -, x = 1/2, y = 1712 paths that make a with velocity va 10. "J : f ( x , y , Z ) = xy - 22, x = rcos0,...

BA 1605: Midterm Recap (Due: Feb. 27, 2015) Name _____________________________ 50 Student ID _____________________________ Section 01B 10:00~11:20 am Section 02B 01:00~02:20 pm [Questions 4 ~ 7] The...

Please #27, 29, 31, 33, 35, 37, 39, 41,45, 57, 61, 69, 77 1-4 Evaluate the integral using integration by parts with the 9. f w In w dw 10. In x -2 . dx indicated choices of u and du. 1. (xedx; u = x,...

Please #1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25 1-4 Evaluate the integral using integration by parts with the 9. f w In w dw 10. In x -2 . dx indicated choices of u and du. 1. (xedx; u = x, du...

Please #27, 29, 31, 33, 35, 37, 39, 41,45, 57, 61, 69, 77 25. z'e' dz 26. (arcsin x)2 dx (b) Use part (a) to evaluate ] cos x dx. (c) Use parts (a) and (b) to evaluate ( cos x dx. 27 . ( (1 + x ) e 3...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

A 12-pack of Omni-Cola (mass 4.30 kg) is initially at rest on a horizontal floor. It is then pushed in a straight line for 1.20 m by a trained dog that exerts a horizontal force with magnitude 36.0...

What assumptions are necessary for a market to be perfectly competitive? In light of what you have learned in this chapter, why is each of these assumptions important?

The Tasmanian Visitor Survey presents data in an analyser database on a number of aspects of tourism, including attractions visited by tourists aged 14 or over. The most visited attractions by...

Is your monthly spending less than your income? Yes/No

For the linear function f(x) = -4x + 3, (a) Find the slope and y-intercept. (b) What is the average rate of change of f? (c) Determine whether f is increasing, decreasing, or constant. (d) Graph f.

Find the distance between the points P = (-1, 3) and Q = (4, -2). Find the midpoint of the line segment P to Q.

Which of the following functions might have the graph shown? (a) f(x) = 3x + 1 (b) g(x) = -2x + 3 (c) H(x) = 3 (d) F(x) = -4x - 1 (e) G(x) = -2/3 x + 3 4

Five types of adjusting journal entries (max 5 to 7 slides). (.ppt) Please help in making this presentation.

FIFO method. i have missing information.. & not entirely sure the input i already have is correct or not Required information Problem 20-9AA FIFO: Process cost summary, equivalent units, cost...

Explain why a firm might prefer a stock repurchase rather than an increase in the firm's regular dividend.