Question: Develop an elegant approach to the exponential and logarithm functions. Define a function G for x > 0: This exercise proceeds as if we didnt

Develop an elegant approach to the exponential and logarithm functions. Define a function G for x > 0:

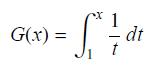
G(x) = S JI 1 - dt

This exercise proceeds as if we didn’t know that G(x) = ln x and shows directly that G has all the basic properties of the logarithm. Prove the following statements.

ab 1 4 + d^ = 5 / dt (b) G(ab) = G(a) + G(b). Break up the integral from 1 to ab into two integrals and

G(x) = S JI 1 - dt

Step by Step Solution

★★★★★

3.49 Rating (176 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Let u ta Then du dta ua 1 uab b and b Using part a ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

1. Contrast McGregor's Theory X and Theory Y assumptions about people. 2. What types of managers have you dealt with in your organization? 3. Assess why there is a predominance of Theory X or Theory...

Use Exercise 116 to prove the following statements. (a) G has an inverse with domain R and range {x : x > 0}. Denote the inverse by F. (b) F(x + y) = F(x)F(y) for all x, y. It suffices to show that...

Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...

Math 1330 Precalculus Electronic Homework (EHW 2) Algebra Review You have 2 electronic homework assignments over Algebra Review (EHW 1 and EHW 2); be careful about choosing the correct EMCF title...

8.1. Dulles Electric Company buys 1 million tons of coal annually to burn at its power plant. The company wants to invest in a unit train that will haul coal from the mine to the power house, where...

6.1. Carbondale Company has the following credit policy 2/10, net 30. Carbondale also charges 1% per month interest on all accounts after 30 days. The following table shows the collection schedule of...

1. Calculate the sample size needed given these factors: one-tailed t-test with two independent groups of equal size small effect size (see Piasta, S.B., & Justice, L.M., 2010) alpha =.05 beta = .2...

X 951961..: "Towards a winter tra X + - C ximera.osu.edu/mooculus/higherOrderDerivativesAndGraphs/exercises/exerciseList/higherOrderDerivativesAndGraphs/exercises/higherOrderDerivatives1 H Men Custom...

Applied Mathematics and Computation 95 (1998) 181192 Love dynamics: The case of linear couples Sergio Rinaldi 1 Centro Teoria dei Sistemi, CNR, Politecnico di Milano, Via Ponzio 34/5, 20133 Milan,...

Article review: see attached Abstract: One paragraph Literature Review: a brief no more than one page discussion of the important (top three articles) literature and the findings of that literature....

Find the number of 90 angles in XeF, molecules. Backspace 7 8 9 4 5 6 1 2 3

Suppose r RF = 9%, r M = 14%, and X = 1.3. a. What is r X , the required rate of return on Stock X? b. Now suppose r RF (1) Increases to 10 percent (2) Decreases to 8 percent. The slope of the SML...

3. The table below shows the mass of's grony y pupils and their respective intelligence (10) score 75 62 56 66 Mass (kg) 113 94 95 111 IQ score 67 47 82 56 Mass (kg) 102 101 106 115 91 IQ score (i)...

14. Save and invest amounts suffi cient to fund a fi nancially successful retirement.

For b > 0 with b 1, what are the domain and range of f(x) = log b x and why?

Express 2 5 using base e.

Find three intervals on which f is one-to-one, making each interval as large as possible. y. %3Dfx) + -3 -2 -1

Jack Sparrow Company purchases inventory from Terminator Inc. by issuing a 3 - month, zero - interest - bearing note on November 1 , 2 0 2 3 . Jack Sparrow Company provides the following details...

You manage an equity fund with an expected risk premium of 10% and an expected standard deviation of 14%. The rate on Treasury bills is 6%. Your client chooses to invest $60,000 of her portfolio in...

HEIR JORDAN CORPORATION Income Statement Sales Costs $48,500 34,500 Taxable income Taxes (25%) $14,000 3,500 Net income $10,500 Dividends Addition to retained $2,514 7,986 earnings The balance sheet...