Find a function F(x, y) satisfying and use the result of Exercise 52 to evaluate for R
Question:
Find a function F(x, y) satisfying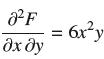 
and use the result of Exercise 52 to evaluate 
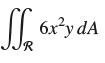for R = [0, 1] × [0, 4].
Data From Exercise 52
Prove the following extension of the Fundamental Theorem of Calculus to two variables: If ∂2F/∂x ∂y = ƒ(x, y), then
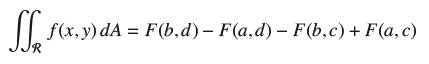
where R = [a, b] × [c, d].
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
xy We integrate with respect to x taking zero as the consta...View the full answer
Answered By
Divya rana
Nuclear Engineering fresh graduate from Gadjah Mada University. Highly motivated, responsible, and dedicated individual who is committed to achieving success and making a positive impacts. Possess strong passion and excellent skill in mathematical modeling, physics, programming, particularly in computation and simulation.
I also enjoy teaching and sharing my knowledge. With my experience in programming, i love making tool or
visualization to make learning more interactive and enjoyable.
I've several achievement including silver medal in 2020 National Physics Olympiad, 2nd Place in 2022 Scientific Paper Competition, and 1st Place in Statistics and Math Olympiad.
I've been an instructor in National Science Olympiad Training, teaching students preparing for national science olympiad.
In my university, i've been a lab assistant for Computer Programming, and course assistant for Numerical Method.
0 Reviews
10+ Question Solved
Related Book For 
Question Posted:
