Question: FTC I asserts that Use FTC II to give a new proof of FTC I as follows. So f(t) dt = F(b) - F(a)

FTC I asserts that 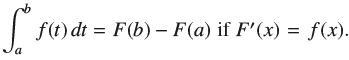 So f(t) dt = F(b) - F(a) if F'(x) = f(x). a Use FTC II to give a new proof of FTC I as follows.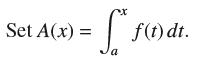 Set A(x) = f(t) dt. Ja

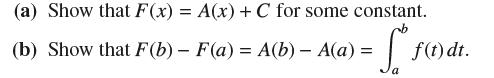
(a) Show that F(x) = A(x) + C for some constant. S (b) Show that F(b)- F(a) = A(b) - A(a) = f(t) dt.

So f(t) dt = F(b) - F(a) if F'(x) = f(x). a

Step by Step Solution

★★★★★

3.57 Rating (150 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

Let Fx fx and Ax f ft dt a Then by the FTC Part ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...

Q:

1. How strong are the competitive forces confronting J. Crew in the market for specialty retail? Do a [Michael Porter] five-forces analysis to support your answer. (see chapter 3 in the textfor...

Q:

NATURAL CEREALS SITUATION II The Meeting Fortunately, Sally and Joe were able to schedule a meeting with Tom for that afternoon. As they walk into Toms office, Sally feels a little uneasy. She...

Q:

x Course Home X P Quiz 2A x 5 New Tab X + pearson.com/Student/PlayerTest.aspx?testld=252135103¢erwin=yes 1901 Alexandra Shoffler 06/09/23 Question 1 of 10 This quiz: 100 point(s) possible This...

Q:

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

Q:

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

Q:

f a processor exhibited one branch delay slot how would you reorder (and possibly modify) the instructions in the following loop to gain a performance advantage? loop ldr r2,r3,#4 % r2=load(r3),...

Q:

Digital Communication I X A B C D Y Hosts X and Y are communicating through the data network provided by the switches A, B, C and D and the links interconnecting them as shown above. Initially all...

Q:

Let i and j be positive integers. (i) Prove that there exist natural numbers a and b such that ai = bj+gcd(i, j). You may use standard results provided that you state them clearly. [4 marks] (ii) Let...

Q:

ttth Suppose that the sequence of bags {Bn | n N} is recursively enumerated by the computable function e(n, x) = fn(x), [7 marks] Hence prove that the set of all recursive bags cannot be recursively...

Q:

You put $10,000 into two accounts. Account 1 pays simple interest of 10%. Account 2 pays compound interest of 10% 1. Determine the value of Account 1 at the end of 50 years 2. Determine the value...

Q:

A fabric mill has developed the following forecasts (in hundred bolts of cloth). The mill has a normal capacity of 275 units (a unit=hundred bolts) per month, and employs 275 workers. Regular labour...

Q:

The National Conference of Commissioners on the Uniform Probate Code has drafted two uniform acts pertaining to probate and trusts. Group of answer choices True False

Q:

As a marketer, how could you use this information to promote lowerpriced goods against competitors selling higher-priced goods? Use further examples to justify your argument.

Q:

How high is the arch of Problem 43 at a distance 2 feet to the right of the center? In Problem 43 A doorway in the shape of an elliptical arch (a half-ellipse) is 10 feet wide and 4 feet high at the...

Q:

How long is the lams rectum (chord through the focus perpendicular to the major axis) for the ellipse x2/a2 + y2/b2 = 1?

Q:

Determine the length of the latus rectum of the hyperbola x2/a2 - y2/b2 = 1.

Q:

using System; using System.Windows.Forms; namespace LoginFormApp { public partial class Form 1 : Form { public Form 1 ( ) { InitializeComponent ( ) ; / / Populate the gender ComboBox...

Q:

Business Ethic subject The Commercialism versus Professionalism case raises issues about: The future of the accounting profession Low-ball bidding for audit services Pressures to compromise ethical...

Q:

Gelb Company currently manufactures 59,000 units per year of a key component for its manufacturing process. Variable costs are $7.35 per unit, fixed costs related to making this component are $89,000...