Generalize Exercise 86; that is, use induction (if you are familiar with this method of proof) to prove that for all n ≥ 0,

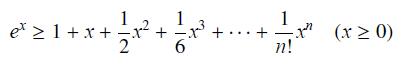
Exercise 86

Recall the following property of integrals: If ƒ(t) ≥ g(t) for all t ≥ 0, then for all x ≥ 0,

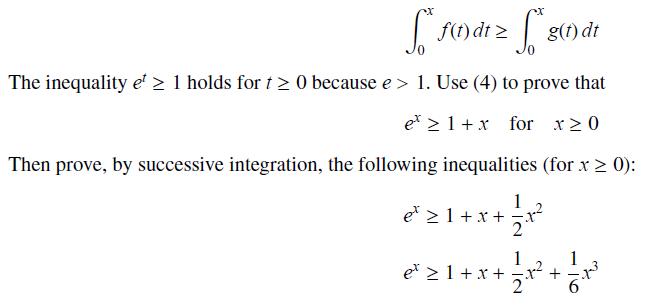
1 ex > 1 + x + - x2 > 2 + + ... + 1 6 1 - n! (x > 0)