If '(c) = 0 and (c) is neither a local min nor a local max, must x = c be a point of inflection? This

If ƒ'(c) = 0 and ƒ(c) is neither a local min nor a local max, must x = c be a point of inflection? This is true for “reasonable” functions (including the functions studied in this text), but it is not true in general. Let

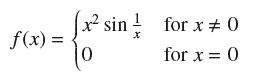
(a) Use the limit definition of the derivative to show that ƒ'(0) exists and ƒ'(0) = 0.
(b) Show that ƒ(0) is neither a local min nor a local max.
(c) Show that ƒ'(x) changes sign infinitely often near x = 0. Conclude that x = 0 is not a point of inflection.

f(x) = x sin / for x = 0 for x = 0