Question: In Exercises 17 and 18, let y(t) be a solution of the logistic equation where A > 0 and k > 0. (a) Differentiate Eq.

In Exercises 17 and 18, let y(t) be a solution of the logistic equation

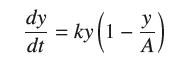
dt = ky(1 A

where A > 0 and k > 0.

(a) Differentiate Eq. (9) with respect to t and use the Chain Rule to show that

( x - ) 4 = 7/1

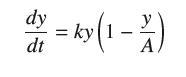
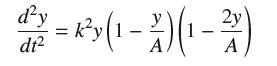
d=2(1-2)(1-2) 2y A

(b) Show that the graph of the function y is concave up if 0 < y < A/2 and concave down if A/2 < y < A. (c)

dt = ky(1 A

Step by Step Solution

★★★★★

3.43 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a The derivative o... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

In Exercises 17 and 18, let y(t) be a solution of the logistic equation where A > 0 and k > 0. Let y = A/1 e kt /B be the general nonequilibrium solution to Eq. (9). If y(t) has a vertical asymptote...

Q:

Show that (9) in Sec. 12.6 with coefficients (10) is a solution of the heat equation for t > 0 assuming that f(x) is continuous on the interval 0 ¤ x ¤ L and has one-sided derivatives...

Q:

1. Mr. Jones is the human owner of a farm called Manor Farm. Describe what kind of personality Mr. Jones has and include two quotations to prove your point. 2. Old Major is an elderly pig who is very...

Q:

Problems : 9,11,24,25,26 Direction : in the exercices 9 and 11 find a basis for the eigenspace corresponding to each listed eigenvalueHello can I have some help here please. Can you write on a sheet...

Q:

2.7. Explicit Solutions to Dierential Equations 109 power (kw) 20 15 10 5 0 08:00 10:00 12:00 14:00 16:00 time 18:00 2.7 Explicit Solutions to Dierential Equations In the very rare case in which an...

Q:

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

Q:

Can you please help me with number 21. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Open with Chapter 5 Linear Systems...

Q:

Can you please help me with number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Linear Systems quations 406 The...

Q:

Can you please help me with number 12 and number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.6 Problems Find...

Q:

Can you please help me with number 31. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.7 Matrix Exponentials and Linear...

Q:

Solve the given initial value problem and determine at least approximately where the solution is valid. (12x + y 1) dx (18y x) dy = 0, y(1) = 0 Y the solution is valid as long as x Choose one...

Q:

A coil has 5000 turns of wire and a resistance of 400 ohms , and the coil is rewound same weight of wire which have 13000 turns. How many ohms have new coil have ?

Q:

abled: Midterm 2 i Saved Preferred stock creates tax shields that reduce the cost of capital. True or False

Q:

A15.12 What happens to cash flow when working capital increases? (Section 15.4)

Q:

Prove the identity. sinh(-x) = -sinh x (This shows that sinh is an odd function.)

Q:

(a) Explain how we know that the given equation must have a root in the given interval. (b) Use Newtons method to approximate the root correct to six decimal places. 3x* 8x + 2 = 0, [2, 3]

Q:

Find dy/dx by implicit differentiation. x 4 + x 2 y 2 + y 3 = 5

Q:

Explain with neat sketch Bridgeman correction for metals

Q:

promotion can assist sales people in finding likely sales prospects ? true or false

Q:

Which of the following is not a risk factor? Unavailability of qualified staff. Occurrence of unforeseen disputes. Materials shortages. Exchange rates