Question: In the notation of Exercise 66, give an example where L exists but neither A nor B exists. Data From Exercise 66 Assume that the

In the notation of Exercise 66, give an example where L exists but neither A nor B exists.


Data From Exercise 66

Assume that the following limits exist:

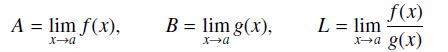
A = lim f(x), xa B = lim g(x), xa f(x) xa g(x) L = lim

Prove that if L = 1, then A = B. You cannot use the Quotient Law if B = 0, so apply the Product Law to L and B instead.

A = lim f(x), xa B = lim g(x), xa f(x) xa g(x) L = lim

Step by Step Solution

★★★★★

3.46 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

Suppose Then ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

Give an example where (f (x) + g(x)) exists but neither f(x) nor g(x) exists. lim

Q:

Fullerton Waste Management purchased land and a warehouse for $750,000. In addition to the purchase price, Fullerton made the following expenditures related to the acquisition: broker's commission,...

Q:

The FBIs Uniform Crime Reporting (UCR) program gathers crime data from more than 17,000 law enforcement agencies throughout the United States. The Crime data set contains crime counts for several...

Q:

chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS The purpose of this chapter is to introduce you to matrix algebra, which has many applications. You are already familiar with several algebras:...

Q:

Microkernel operating systems aim to address perceived modularity and reliability issues in traditional "monolithic" operating systems. (i) Describe the typical architecture of a microkernel...

Q:

(a) How does the use of condition codes complicate the implementation of a superscalar processor that supports out-of-order execution? [4 marks] (b) A branch predictor with a high prediction accuracy...

Q:

PLEASE COMPLETE NO LATER THAN 10/07 @8:00AM Each question(1,2,& 3) must be a minimum of 200 words. Please make answers detailed and knowledgeable based off the attached reading. ARE YOU ABLE TO...

Q:

HW 12, MAT 312/AMS 351: SPRING 2017 Problem 1. (1) Set H = {4a + 6b | a, b Z} Z. Show that H is a subgroup of Z. (2) Is H cyclic? Problem 2. Write down all the cyclic subgroups of the following...

Q:

Exercise Set 5.3: Graphs of the Tangent, Cotangent, Secant, and Cosecant Functions (f) Give an interval, if one exists, on which f ( x ) = tan ( x ) is increasing. Then give an Answer the following....

Q:

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

Q:

A firm has a $100,000 2-year variable interest loan with 180 day payment frequency. The firm decided to purchase a cap with X=6% and sells a floor with X=4%. The cap's price is $15,000 and the...

Q:

Which of the following statements are true concerning signconventions for image formation? Check all that apply. A virtual image has a positive image distance; a real image hasa negative image...

Q:

With reference to the data in Table 18.5, explain why prices in Iran were generally higher in 2013 than in 2012.

Q:

12.6. Outline the importance of coordinating the business plan segments

Q:

(a) If the symbol [ ] denotes the greatest integer function defined in Example 10, evaluate (b) If n is an integer, evaluate (c) For what values of does limxa [x] exist? lim, xl lim X lim x

Q:

(a) If the symbol [ ] denotes the greatest integer function defined in Example 10, evaluate (b) If n is an integer, evaluate (c) For what values of does limxa [x] exist? lim, xl lim X lim x

Q:

If f(x) = [x] + [-x], show that limx2 f(x) exists but is not equal to f(2).

Q:

https://www.chegg.com/homework-help/questions-and-answers/ground-truth-target-function-d-e-f-f-x-todo-use-first-5-datasets-generate-4-plots-figure-o-q108455785 I am getting an error for this code....

Q:

Problem 9-7 WACC Shi Import-Export's balance sheet shows $300 million in debt, $50 million in preferred stock, and $250 million in total common equity. Shi's tax rate is 30%, r d = 6%, r ps = 7.2%,...

Q:

Coca Cola shares are currently trading at $45.15 per share. Earnings per share (EPS) for Coca-Cola is $2.32 year. Dividend per share is expected to be $1.64 per share. Calculate the P/E ratio for...