In this exercise, we show that the vector field F in Figure 15 is not conservative. Explain the following statements:
(a) If a potential function ƒ for F exists, then the level curves of ƒ must be vertical lines.

(b) If a potential function ƒ for F exists, then the level curves of ƒ must grow farther apart as y increases.
(c) Explain why (a) and (b) are incompatible, and hence ƒ cannot exist.

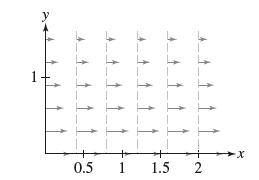
0.5 1 1.5 2 x