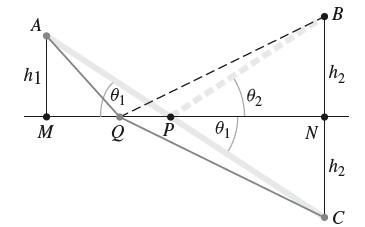
Question: In this exercise, we use Figure 42 to prove Herons principle of Example 7 without calculus. By definition, C is the reflection of B across
In this exercise, we use Figure 42 to prove Heron’s principle of Example 7 without calculus. By definition, C is the reflection of B across the line MN (so that BC is perpendicular to MN and BN = CN). Let P be the intersection of AC and MN. Use geometry to justify the following:

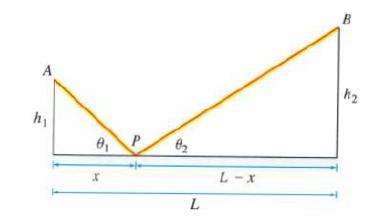
Example 7

= 0. (a) and NC are congruent and (b) The paths APB and APC have equal length. (c) Similarly, AQB and AQC have equal length. (d) The path APC is shorter than AQC for all Q # P. Conclude that the shortest path AQB occurs for Q = P.
Step by Step Solution
3.43 Rating (156 Votes )
There are 3 Steps involved in it
a By definition BC is orthogonal to QM so triangles APNB and APNC ... View full answer

Get step-by-step solutions from verified subject matter experts


