Question: Let a, b, c be nonzero vectors. Assume that b and c are not parallel, and set v = ax (bx c), (a) Prove that:

Let a, b, c be nonzero vectors. Assume that b and c are not parallel, and set

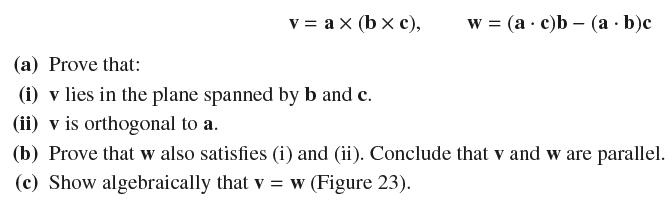
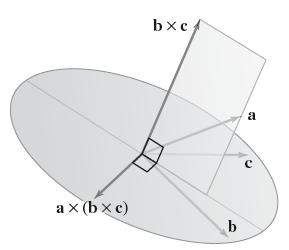
v = ax (bx c), (a) Prove that: (i) v lies in the plane spanned by b and c. (ii) v is orthogonal to a. w = (a.

ax(bxc) bxc b a C

v = ax (bx c), (a) Prove that: (i) v lies in the plane spanned by b and c. (ii) v is orthogonal to a. w = (a c)b (a . b)c . (b) Prove that w also satisfies (i) and (ii). Conclude that v and w are parallel. (e) Show algebraically that v = w (Figure 23).

Step by Step Solution

★★★★★

3.37 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Since v is the cross product of a and another vector b c then v is orthogonal to a Furthermore v i... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Let a and b be nonzero vectors in Rn. a) If (t) = a + tb for t R, show that for each to, t0, t1, t2 R with t1, t2 t0, the angle between (t0) - (t0) - (t0) and (t2) - (t0) is 0 or . b) If is the...

In our development of consumer theory, we made a big point about the fact that neoclassical economics does not put much stock in the idea of cardinally measuring utility (in terms of units of...

Assume that the universal set U is the set of all people living in the United States. Let A be the set of all U.S. citizens, let B be the set of all children under 5 years of age, let C be the set of...

ni- 49. Use the cross product to find the area of the triangle in the xy-plane WO defined by (1, 2), (3, 4), and (-2, 2). X () nolupo ads pulos le- 50. Use the cross product to find the area of the...

77. Let a, b, c be nonzero vectors. Assume that b and c are not parallel, and set v=ax (bxc), w (a c)b (a b)c a. Prove that: i. v lies in the plane spanned by b and c. ii. v is orthogonal to a. b....

Use Exercise 77 to prove the identity Data From Exercise 77 Let a, b, c be nonzero vectors. Assume that b and c are not parallel, and set (axb)xc-ax(bxc) = (a - b)c - (b.c)a

Recall that the area of a parallelogram with base b and altitude h is given by bh, and the volume of a parallelepiped is given by the area of its base times its altitude. a) Let a, b R3 be nonzero...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

please only solve question number 9 only [IV, $4] FUNCTIONS DEPENDING ON DISTANCE FROM ORIGIN 109 110 THE CHAIN RULE AND THE GRADIENT [IV, $4] IV, $4. EXERCISES 7. Parametrizatione (x*/a*) + (y*/b')...

Give Correct ANSWERS Human-Computer Interaction (a) If you had been one of the original inventors of the WIMP interface, and engineers on the technical team had been sceptical about the advantages...

Suppose that the 33rd percentile of a normal distribution is equal to 656 and that the 97.5th percentile of this normal distribution is 896. Find the mean m and the standard deviation s of the normal...

Refer to the original data in P22-30B and the revisions presented in P22-34B. Requirements 1. Prepare the schedule of budgeted cash collections from customers for April and May. 2. Prepare the...

keep in mind that a dividend can only be given if a) the dividend will not make the compnay insolvent b) the corporation can still cover liabilities after the divident is paid c) the company has made...

8.7 If shear-strength measurements have a standard deviation of 10 psi, how many test welds should be used in the sample if the sample mean is to be within 1 psi of the population mean with...

An object of mass m (in grams) attached to a coiled spring with damping factor b (in grams per second) is pulled down a distance a (in centimeters) from its rest position and then released. Assume...

The distance d (in meters) of the bob of a pendulum of mass m (in kilograms) from its rest position at time t (in seconds) is given. The bob is released from the left of its rest position and...

senior tax specialist test hr block

You are considering investing in a start up project at a cost of $75,000. You expect the project to return $38,000, $25,000 and $55,000 to you in the next three years. Given the cost of capital is...

ATV Co. began operations on March 1 and uses a perpetual inventory system. It entered into purchases and sales for March as shown in the Tableau Dashboard. March Thursday Wednesday Sunday Monday...