Let be a linear map. Prove Eq. (6) in the following steps. (a)For any set D in the uv-plane and any vector u, let

Let Φ be a linear map. Prove Eq. (6) in the following steps.

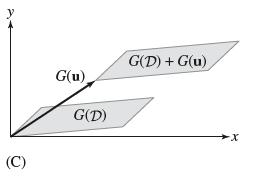
(a) For any set D in the uv-plane and any vector u, let D + u be the set obtained by translating all points in D by u. By linearity, Φ maps D + u to the translate Φ(D) + Φ(u) [Figure 19(C)]. Therefore, if Eq. (6) holds for D, it also holds for D + u.

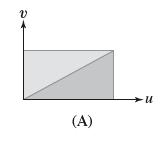
(b) In the text, we verified Eq. (6) for the unit rectangle. Use linearity to show that Eq. (6) also holds for all rectangles with vertex at the origin and sides parallel to the axes. Then argue that it also holds for each triangular half of such a rectangle, as in Figure 19(A). 

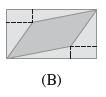
(c) Figure 19 (B) shows that the area of a parallelogram is a difference of the areas of rectangles and triangles covered by steps (a) and (b). Use this to prove Eq. (6) for arbitrary parallelograms.

area(G(D)) = |Jac(G)|area(D)