Let (C, D), and (mathcal{E}) be the oriented curves in Figure 16, and let (mathbf{F}=abla f) be

Question:

Let $C, D$, and $\mathcal{E}$ be the oriented curves in Figure 16, and let $\mathbf{F}=abla f$ be a gradient vector field such that $\int_{C} \mathbf{F} \cdot d \mathbf{r}=4$. What are the values of the following integrals?
(a) $\int_{\mathcal{D}} \mathbf{F} \cdot d \mathbf{r}$
(b) $\int_{\mathcal{E}} \mathbf{F} \cdot d \mathbf{r}$

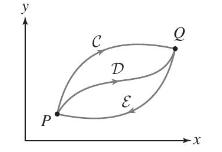
y P C D E Q