Question: Let I = 1 0 x p ln x dx. (a) Show that I diverges for p = 1. (b) Show that if p

Let I =∫10 xp ln x dx.
(a) Show that I diverges for p = −1.
(b) Show that if p ≠ −1, then

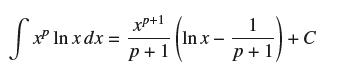
[xnxdx=(x-)+c XP+1 In p+1 1 p+1) +C

(c) Use L’Hôpital’s Rule to show that I converges if p > −1 and diverges if p

[xnxdx=(x-)+c XP+1 In p+1 1 p+1) +C

Step by Step Solution

★★★★★

3.43 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a If p 1 then Let u ln x du 1x dx Then Thus and fx Inx dx c Let p 1 Th... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-7. Ivan sold the following securities during the year and received a Form 1099-B that...

Q:

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-6. On December 12, Irene purchased the building where her store is located. She paid...

Q:

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-4. Ivan and Irene paid the following in 2012 (all by check or can otherwise be...

Q:

868 CHAPTER 15 DIFFERENTIATION IN SEVERAL VARIABLES 5. Let f (x, y) = 12x - yx2 + xy. (c) be ch (a) Show that the critical points (x, y) satisfy the equations max for t y(y - 2x + 1) =0, x ( 2y - x +...

Q:

Math 104A Homework #3 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

Q:

11. [-/1 Points] DETAILS MY NOTES SCALCET9 11.1.035. Determine whether the sequence converges or diverges. If it converges, find the limit. (If the sequence diverges, enter DIVERGES.) a = e-7/Vn lim...

Q:

need help with my worksheetsss MCV4U Unit 2 - Activity 2 The Derivatives of Polynomial Functions We have seen that derivatives of functions are of practical use because they represent instantaneous...

Q:

7/4/23, 11:16 PM Homework 8.7-Anh Nguyen Use a table of integrals to determine tv7t+ 19 at. Click here to view page 1 of the integral table. " Click here to view page 2 of the integral table. 14...

Q:

Please help me with the following questions. Thanks in advance. QUESTION 1 tan ( 5x) Use the Quotient Rule to find f '(x) given f (x) = x2 + 7 For the toolbar, press ALT+F10 (PC) or ALT+FN+F10 (Mac)....

Q:

11. DETAILS SCALCET9 7.5.073. Evaluate the integral. (Use C for the constant of integration.) 5 sin(2x) dx 1 + cos (x) -5 arctan ( cos (x) ) + C + Show My Work (Optional) ? Viewing Saved Work Revert...

Q:

Please answer this question in biochemisty Draw the hydrogen bond(s) between the following two sets of bases. The letter "R" represents the rest of the nucleotide. The bases are positioned...

Q:

The FED Reserve Bank in Dallas manages the banknote supply/circulation in Texas which we can assume to be isolated from the other states. Suppose that the Dallas FED actually does not print money but...

Q:

an 8 % bond that matures in two years has a WTM 7 % what assumptions can we make?

Q:

12. Engineering: Roller Bearings Two processes for manufacturing large roller bearings are under study. In both cases, the diameters (in centimeters) are being examined. A random sample of 21 roller...

Q:

A strain of E-coli Beu 397-recA441 is placed into a nutrient broth at 30 Celsius and allowed to grow. The following data are collected. Theory states that the number of bacteria in the petri dish...

Q:

Is the set of ordered pairs 1(1, 3), (2, 3), (-1, 2)) a function? Why or why not?

Q:

In problem, for the given functions f and g find: (a) (f g)(2) (b) (g f)(-2) (c) (f f)(4) (d) (g g)(-1) f(x) = 3x - 5; g(x) = 1 - 2x 2

Q:

Let D be a dictionary ADT with N items implemented with a AVL tree. Show how to implement the following method countAllInRange(k1,k2) for D. This method should compute and return athe number of keys...

Q:

Please help with these Data Structure questions 2-what class inherits the members of another class? a)base class b)super class c)abstract class d)subclass 3-(true/False) all the items in a list must...

Q:

Computech Corporation is expanding rapidly and currently needs to retain all of its earnings; hence, it does not pay dividends. However, investors expect Computech to begin paying dividends,...