Question: Let (mathbf{F}) be a vector field whose curl and divergence at the origin are [ operatorname{curl}(mathbf{F})(0,0,0)=langle 2,-1,4angle, quad operatorname{div}(mathbf{F})(0,0,0)=-2 ] Estimate the flux of (mathbf{F})

Let \(\mathbf{F}\) be a vector field whose curl and divergence at the origin are
\[
\operatorname{curl}(\mathbf{F})(0,0,0)=\langle 2,-1,4angle, \quad \operatorname{div}(\mathbf{F})(0,0,0)=-2
\]

Estimate the flux of \(\mathbf{F}\) through the box of side 0.5 in Figure 4 . Does the result depend on how the box is oriented relative to the coordinate axes?

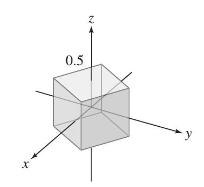
0.5 C y

Step by Step Solution

★★★★★

3.46 Rating (162 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To estimate the flux of the vector field mathbfF through the box we can make use of the provided information about the curl and divergence of mathbfF ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Let \(\mathbf{F}\) be a vector field whose curl and divergence at the origin are \[ \operatorname{curl}(\mathbf{F})(0,0,0)=\langle 2,-1,4angle, \quad \operatorname{div}(\mathbf{F})(0,0,0)=-2 \]...

2. [-/1 Points] DETAILS SCALCET9 16.8.006. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Use Stokes' theorem to evaluate curl ( F ) . ds . F(x, y, z) = e *yi+ e*j + x2zk, S is the half of the ellipsoid...

Let \(\mathbf{F}\) be a vector field on an open, connected domain \(\mathcal{D}\) with continuous second partial derivatives. Which of the following statements are always true, and which are true...

Let \(\mathbf{F}\) be the vector field \[ \mathbf{F}(x, y)=\left\langle\frac{x}{x^{2}+y^{2}}, \frac{y}{x^{2}+y^{2}}ightangle \] and assume that \(C_{R}\) is the circle of radius \(R\) centered at the...

Let \(\mathbf{F}\) be a vector field and \(\Phi(u, v)\) a parametrization of a surface \(\mathcal{S}\), and set \(\mathbf{N}=\mathbf{T}_{u} \times \mathbf{T}_{v}\). Which of the following is the...

Let \(\mathbf{F}\) be a continuously differentiable vector field in \(\mathbf{R}^{3}, Q\) a point, and \(\mathcal{S}\) a plane containing \(Q\) with unit normal vector e. Let \(C_{r}\) be a circle of...

Let \(f(x, y)=x+\frac{x}{x^{2}+y^{2}}\). The vector field \(\mathbf{F}=abla f\) (Figure 5) provides a model in the plane of the velocity field of an incompressible, irrotational fluid flowing past a...

The vector field \(\mathbf{F}(x, y)=\left\langle\frac{x}{x^{2}+y^{2}}, \frac{y}{x^{2}+y^{2}}ightangle\) is defined on the domain \(\mathcal{D}=\{(x, y) eq(0,0)\}\). (a) Is \(\mathcal{D}\) simply...

A peacock is sitting on the top of a pillar, which is 9 m high. From a point 27 m away from the bottom of the pillar, a snake is coming to its hole at the base of the pillar. Seeing the snake the...

Use the partial equilibrium framework to explain the meaning of trade diversion. Is there a policy that allows countries in a custom union to avoid the costs implied by trade diversion?

Goodwill is not amortized but is tested at least annually and written down to current fair value if found to be impaired, and written up to fair value if the fair value increases. True False

1. When did Auciello become aware of the question about the unions majority support? When did Auciello act on that question?

Find the Taylor series for f (x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that R n (x) 0.] Also find the associated radius of convergence. f(x) =...

Find the Taylor series for f (x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that R n (x) 0.] Also find the associated radius of convergence. 2 f(x) =...

C++ Implement a B-Tree Insert within a program.

Assume that a commercial real estate whose monthly rent is USD 6.000 is to be sold at USD 4.000.000 Inflation rate has been 10% and the nominal interest rate 16% on the average for the last 15 years....

puppys paradise is a manufacturer of dog treats and toys. they have become so successful that they have decided to market their products overseas. they have decided that, since their company is doing...