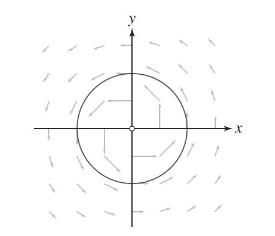
Let \(\mathbf{F}\) be the vortex field (Figure 24):

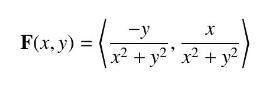
Let \(C\) be a curve in polar form \(r=f(\theta)\) for \(\theta_{1} \leq \theta \leq \theta_{2}\) [Figure 25(B)], parametrized by \(\mathbf{r}(\theta)=\) \((f(\theta) \cos \theta, f(\theta) \sin \theta))\) as in Exercise 60.
(a) Show that the vortex field in polar coordinates is written \(\mathbf{F}(r, \theta)=r^{-1}\langle-\sin \theta, \cos \thetaangle\).
(b) Show that \(\mathbf{F} \cdot \mathbf{r}^{\prime}(\theta) d \theta=d \theta\).
(c) Show that \(\int_{C} \mathbf{F} \cdot d \mathbf{r}=\theta_{2}-\theta_{1}\).

-) =(++2 ) 1x + y x + y F(x, y) =