Let \(\mathcal{D}\) be the region bounded by a simple closed curve \(C\). A function \(\varphi(x, y)\) on \(\mathcal{D}\) (whose second-order partial derivatives exist and are continuous) is called harmonic if \(\Delta \varphi=0\), where \(\Delta \varphi\) is the Laplace operator defined in Eq.(12).

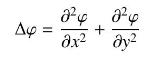
Show that \(f(x, y)=x^{2}-y^{2}\) is harmonic. Verify the mean-value property for \(f(x, y)\) directly [expand \(f(a+r \cos \theta, b+r \sin \theta)\) as a function of \(\theta\) and compute \(\left.I_{\varphi}(r)ight]\). Show that \(x^{2}+y^{2}\) is not harmonic and does not satisfy the mean-value property.

8 _0 Aq = + x2 y2