Question: Let (mathcal{T}) be the triangular region with vertices ((1,0,0),(0,1,0)), and ((0,0,1)) oriented with upward-pointing normal vector (Figure 16). Assume distances are in meters. Calculate the

Let $\mathcal{T}$ be the triangular region with vertices $(1,0,0),(0,1,0)$, and $(0,0,1)$ oriented with upward-pointing normal vector (Figure 16). Assume distances are in meters.

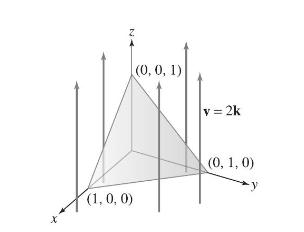
X (1,0,0) (0, 0, 1) v = 2k (0, 1, 0) -y

Calculate the flow rate through $\mathcal{T}$ if $\mathbf{v}=-\mathbf{j} \mathrm{m} / \mathrm{s}$.

X (1,0,0) (0, 0, 1) v = 2k (0, 1, 0) -y

Step by Step Solution

★★★★★

3.33 Rating (162 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

We compute the flow rate through mathcalT Since the unit normal vec... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

mary is itimizing deductions and pays the following amounts for her home during the year 2023, 2600 real state taxes, 6890 mortgage, 1000 home owner insurance premiums, 11200 mortgage insurance...

The Cherry & White Bike Company is a small closely-held company with two owners. Its two owners, Charlotte and George, have decided to expand the business. You are CWBs accountant. Your...

Let $\mathcal{T}$ be the triangular region with vertices $(1,0,0),(0,1,0)$, and $(0,0,1)$ oriented with upward-pointing normal vector (Figure 16). Assume distances are in meters. A fluid flows...

Let 7 be the triangular region region with vertices (1, 0, 0), (0. 1, 0), and (0, 0, 1) oriented with upward-pointing normal vector. Assume distances are in meters. (0, 0, 1) V (0, 1, 0) (1, 0. 0)...

Please help!! Let 7 be the triangular region region with vertices (1, 0, 0), (0. 1, 0), and (0, 0, 1) oriented with upward-pointing normal vector. Assume distances are in meters. (0, 0, 1) V (0, 1,...

ANSWERS ONLY Construct the complementary graph (draw the actual graph) of the following graph representation. Use vertex labels a,b,c,d,e,f when constructing your graph. O O O HO 0 O 10 1 0 0 1...

Using DiPasquale and Wheaton?s 4 quadrant model of the property market as a framework and your knowledge of property cycles , discuss your understanding of the current real estate markets in ONE...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

MA 261 PRACTICE PROBLEMS 1. If the line ` has symmetric equations y x1 z+2 2 = 3 = 7 , nd a vector equation for the line `0 that contains the point (2; 1; 3) and is parallel to `. A. ~ = (1 + 2t)~...

806 Chapter Fifteen OPTIMIZATION: LOCAL AND GLOBAL EXTREMA If f is not continuous or the region R is not closed and bounded, there is no guarantee that f achieves a global maximum or global minimum...

The court states that random, violent crime is endemic in todays society. If that is true, then wasnt it foreseeable that a violent assault would occur at the shopping center?

A truck carrying explosive gases either has chains or straps that drag along the ground, or else it has special tires that conduct electricity (ordinary tires are good insulators). Explain why the...

calculate the cost of not taking a 5 / 1 7 net 9 2 discount

Why have DMOs generally moved away from operating wholesale and/or retail travel services?

An endowment is an investment account in which the balance ideally remains constant and withdrawals are made on the interest earned by the account. Such an account may be modeled by the initial value...

Consider the solution of the logistic equation. a. From the general solution show that the initial condition P(0) = 50 implies that C = -ln 5. b. Solve for P and show that P = 0.1t + C, 300 P 300 P...

Consider the general first-order initial value problem y'(t) = ay + b, y(0) = y 0 , for t 0, where a, b, and y 0 are real numbers. a. Explain why y = -b/a is an equilibrium solution and corresponds...

Quantifying threats into the CIA model can help identify risk

Ch. 9 - Cash Collections Homework Thirst Quencher sells plastic bottles to outdoor enthusiasts for $1.25 each. The companys marketing manager prepared the following sales forecast (in dollars) for...

For this question, it is recommended to read section 1 . 5 . 2 of the course text. We refer to the below integer programming formulation of shortest path ( formulation ( 1 . 3 4 ) in the course text...