Let P = (a, b) be a critical point of (x, y) = x 2 + y 4 4xy. (a) First use fx(x, y)

Let P = (a, b) be a critical point of ƒ(x, y) = x² + y⁴ − 4xy.

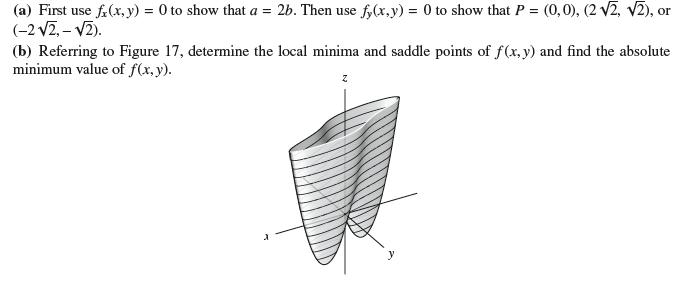
(a) First use fx(x, y) = 0 to show that a = 2b. Then use fy(x,y) = 0 to show that P = (0,0), (2 2, 2), or (-2 2,-2). (b) Referring to Figure 17, determine the local minima and saddle points of f(x, y) and find the absolute minimum value of f(x, y). z