Question: Let P be a plane with equation ax + by + cz = d and normal vector n = (a, b, c). For any point

Let P be a plane with equation ax + by + cz = d and normal vector n = (a, b, c). For any point Q, there is a unique point P on P that is closest to Q, and is such that PQ is orthogonal to P(Figure 12).

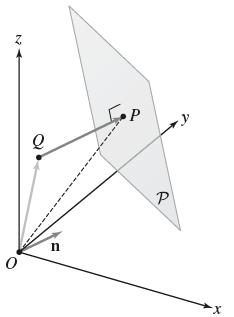
Z 0 Q n P P X

Show that the point P on P closest to Q is determined by the equation

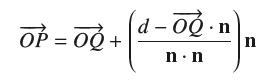
OP = 00 + d - 00.n n.n

Z 0 Q n P P X

Step by Step Solution

★★★★★

3.45 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Since PO is orthogonal to the plane P it is parallel to the vector n a b c which is norm... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

PLEASE IN DETAILED!!! The line graph below uses scalable vector graphics (SVG) to plot the data. The chart uses the element to plot the data, but plots the data in the coordinate system of the data...

1. Positive economics: A. is the same as normative economics. B. is based on opinion polls C. describes opinions and perspectives on how the world should work D. describes how the world does work 2....

Using the following information for McDonovan, Inc's stock, calculate their expected return and standard deviation State 1: Economic boom states 25 % occurrence returns 15% State 2: Economic growth...

Vectors+Dot Product + Cross Product (1) Findavector v with representation given by the directed line segment AB. Draw AB and the equivalent position vector where: A = (0,6, 1), B = (3,4,4) (2) Sketch...

Hi please help me with this and you can take your time. I'm not in a rush and please don't cancel the question. Thanks! Assignment 1. Find the equation of a 2D line which...(3 marks - Knowledge) a)...

This is not a project and/or assignment for marks, as theses are textbook questions, and will not be copying the tutors work/answers. Please answer all the questions in the space provided and in full...

Questions 1. Determine the scalar equation (Ax + By + Cz + D = 0) of a plane through the point (4, 1, 2) and having normal vector = (3, -2, 2). 2. Find the scalar equation of the plane through the...

6. Determine the vertical and horizontal components of each vector. [6 marks] a. 810 N at an incline of 15 from horizontal b. 80 m/s, 60 clockwise from vertical 7. Given a = 2, -10 and b = [-8, 23 ,...

If anyone can help, please do so and thank you! Questions 1. Determine the scalar equation (Ax + By + Cz + D = 0) of a plane through the point (4, 1, 2) and having normal vector , = (3, -2, 2). 2....

You have been assigned to the audit of Fantasy Ride Ltd for the year ended 30 June 2018. You have conducted audit procedures to test the following controls related to Fantasy Rids revenue process. 1....

If f(x) = 3x3 10x3 + 5, graph both f and f. On what intervals is f(x) > 0? On those intervals, how is the graph of f related to its tangent lines? What about the intervals where f(x)

A hedge is a means of increasing or creating exchange gains on an overall basis by entering into a position to offset the risk exposure.

109 Independent random samples were selected from two normally distributed populations with means m1 and m2, respectively. The sample sizes, means, and variances are shown in the following table: a....

Use a graphing utility to solve equation. Express the solution(s) rounded to two decimal places. 6 sin x - e x = 2, x > 0

Use a graphing utility to solve equation. Express the solution(s) rounded to two decimal places. 4 cos(3x) - e x = 1, x > 0

What are the zeros of f(x) = 4 sin 2 x - 3 on the interval [0, 2]?

Which technique is used to prioritize user stories before beginning an iteration?

example of a well structured research

Dunder Mifflin, a paper company, sells their paper to a local grocer. When the grocer sees the sales of toilet paper increase because consumers are buying it in increased quantities, the grocer...