Let \(\partial \mathcal{R}\) be the boundary of the rectangle in Figure 1, and let \(\partial \mathcal{R}_{1}\) and \(\partial \mathcal{R}_{2}\) be the boundaries of the two triangles, all oriented counterclockwise.

(a) Determine \(\oint_{\partial \mathcal{R}_{1}} \mathbf{F} \cdot d \mathbf{r}\) if \(\oint_{\partial \mathcal{R}} \mathbf{F} \cdot d \mathbf{r}=4\) and \(\oint_{\partial \mathcal{R}_{2}} \mathbf{F} \cdot d \mathbf{r}=-2\).
(b) What is the value of \(\oint_{\partial \mathcal{R}} \mathbf{F} d \mathbf{r}\) if \(\partial \mathcal{R}\) is oriented clockwise?

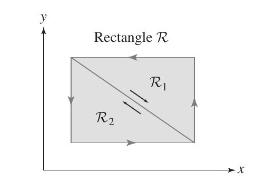
Rectangle R R R