Question: Let r 1 (t) = v 1 + tw 1 and r 2 (t) = v 2 + tw 2 be parametrizations of lines L

Let r₁(t) = v₁ + tw₁ and r₂(t) = v₂ + tw₂ be parametrizations of lines L₁ and L₂. For each statement (a)–(e), provide a proof if the statement is true and a counterexample if it is false.

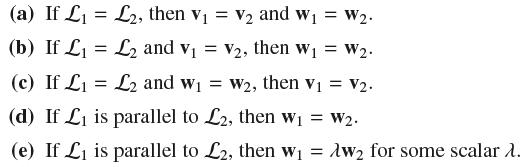
(a) If L : = (b) If L : = (c) If L = L2, then V V and W = W. L2 and v V2, then w = W. = L2 and W W2, then V =

(a) If L : = (b) If L : = (c) If L = L2, then V V and W = W. L2 and v V2, then w = W. = L2 and W W2, then V = V2. (d) If L is parallel to L2, then W = W2. (e) If L is parallel to L2, then w = Aw for some scalar >.

Step by Step Solution

★★★★★

3.34 Rating (148 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a This statement is false Consider the following lines L L2 The line L passes through the points P 1 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Let L1 and L2 be linear transformations from a vector space V into a vector space W. Let {v1, v2 ... vn} be a basis for V. Show that if L1 (v,) = L2 (v) for i = 1, 2 . . . n, then L1 (v) = L2 (v) for...

. Describe how we can prepare 250 mL of 500 ppm Na" form NaCl. 2. Describe how we can prepare 250, mL of 500 ppm Na" form Na;COj 3. Draw a block diagram for the flame-AES: 4. What lunction does the...

Suppose Country A and Country B are trading partners. Country A is operating at full employment and their current account balance is zero (meaning it is not in deficit or surplus). a. Assume that the...

Q1. Let A = {{2}, {2, {2}}} and B = {x, y, y}. Determine if the following statements are true or false. (a) {2} C A T (F (b) 2 EA T (F) (c) |A x B| = 9 T F (d) |P(B)| = 8 T (F Q2. Let R = {(1, 1),...

1(a) Jeniffer has 5 different types of little pony soft toys. The soft-toys characters are Twilight Sparkle (purple colour), Apple Jack (orange colour), Pinkie Pie (pink colour), Fulttershy (yellow...

2 Let R = {(1, 2), (1, 3), (1, 4), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2),(3, 4), (4, 1), (4, 2), (4, 3)} (a) Represent each of the relation in a matrix form. [5 marks] (b) Draw the digraph. [8...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

CCI Linear Algebra Assignment 2 1 Assignment 2 Due Date: 20 October 2015 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Determine whether the statement is true...

MATLAB code plz please use MATLAB for the coding Thank you so much! Consider the inviscid, incompressible flow over a cylinder. Recall from potential flow theory that such a flow can be modeled as...

5 page2.jpg" />9 page6.jpg" />5 page1.jpg" />5 page2.jpg" />6 page2.jpg" />5 page1.jpg" />9 page6.jpg" />9 page5.jpg" />9 page5.jpg" />9 page4.jpg" />9 page3.jpg" />8 page3.jpg" />8 page2.jpg" />8...

(a) Show that the radiation reaction force in the Lorentz-Dirac equation of Problem 16.7 can be expressed alternatively as (b) The relativistic generalization of A6.10) can be obtained by replacing...

Rate the stages of the household life cycle in terms of their probable purchase of the following. Justify your answers. a) Designer jeans b) Trip to Cancun c) Diapers d) Breakfast bars e)...

Supply the missing data for three service companies shown in the table below: Note: Loss omounts should be indicated by o minus sign. Do not round your intermediate calculd \ table [ [ , Company A ,...

=+20-30 K ROI, RI and multinational firms OBJECTIVES 3, 4, 7 Normandy Ltd has a division in Australia and another in Malaysia. The investment in the Malaysian assets was made when the exchange rate...

Find the radius and center of each sphere. 2x 2 + 2y 2 + 2z 2 -8x + 4z = -1

Find the radius and center of each sphere. 3x 2 + 3y 2 + 3z 2 + 6x 6y = 3

The work W done by a constant force F in moving an object from a point A in space to a point B in space is defined as W = F.AB(vector). Use this definition in given Problem. Find the work done by a...

PLEASE EXPLAIN IN DETAILS MORE THAN 400 WORD Explain the difference between Sales Revenue and Net Sales. Show the Income Statement equation and define each element.

The diagram shown is a visual representation of which type of join? Right outer join Inner join Left outer join Full outer join

At the beginning of the year, Vendors, Inc., had owners' equity of $50,825. During the year, net income was $7,025 and the company paid dividends of $4,725. The company also repurchased $9,075 in...