Let S be the hyperboloid x 2 + y 2 = z 2 + 1 and let P = (, , 0) be a point

Let S be the hyperboloid x² + y² = z² + 1 and let P = (α, β, 0) be a point on S in the (x, y)-plane. Show that there are precisely two lines through P entirely contained in S (Figure 18). Consider the line r(t) = (α + at, β + bt, t) through P. Show that r(t) is contained in S if (a, b) is one of the two points on the unit circle obtained by rotating (α, β) through ±π/2. This proves that a hyperboloid of one sheet is a doubly ruled surface, which means that it can be swept out by moving a line in space in two different ways.

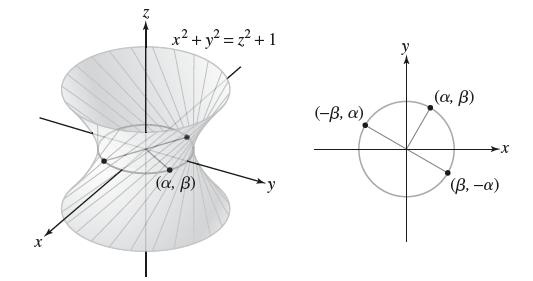
X N x + y = z + 1 (a, B) (-B, ) (, ) -X (B, -)