Let The sine integral function Si is an area function defined by Si(x) = x 0 (t) dt. (a) Explain why Si has critical

Let 

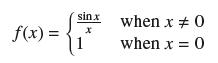
The sine integral function Si is an area function defined by Si(x) = ∫^x ₀ ƒ(t) dt.
(a) Explain why Si has critical points at nπ for all nonzero integers n.

(b) Use Riemann sums to approximate Si(x) for x = π, 2π, . . . , 8π and sketch a graph of Si(x) for 0 ≤ x ≤ 8π.

f(x) = sin.x X when x #0 when x = 0