Let Using polar coordinates, prove that and that does not exist Show that g(x, y) cos 2 and observe that cos can take on any value between 1 and 1 as (x, y) (0, 0) f(x,y) x (x y) and g(x, y) x (x y) ...

Converting to polar coordinates gives T ...

Let Using polar coordinates, prove that and that does not exist. Show that g(x, y) = cos

Question:

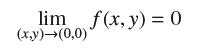Let Using polar coordinates, prove that lim f(x,y)=0 (x,y)(0,0) and that does not exist. Show that g(x, y) = cos²θ and observe that cos θ can take on any value between −1 and 1 as (x, y) → (0, 0).

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Calculus

ISBN: 9781319055844

4th Edition

Authors: Jon Rogawski, Colin Adams, Robert Franzosa

See More Books

Question Posted: Jan 16, 2024 09:00 AM

See More Questions

From Problem 13.8, show that the normalized field pattern of a full-wave (? = ?) antenna is given by Sketch the field pattern. cos(7 cos 0) + 1 F(0) sin 0
Find the value of a that makes the following function differentiable for all x-values. g(x) = (ax, x 3x, - if x < 0 if x 0
Sketch the graph for the given adjacency matrix. 0 1 0 0 1 0 0 0 0 0 0 1 1 0 0 1 0
How does Apple Inc apply Marketing and Advertising To market their product? Direct advertising Indirect Advertising Social Media (Paid Media, Owned Media, Earned Media)
Two humid gas streams are combined in a heated mixing chamber. The first stream contains 23.5 mole% ethane and 76.5% ethylene on a dry basis and enters the chamber at 25C and 105kPa at a rate of...
Which regression equation is best for predicting city fuel consumption? Why? Refer to the accompanying table, which was obtained using the data from 21 cars listed in Data Set 14 in Appendix B. The...
The directors of Bellini plc, a Stock Exchange listed business, are contemplating purchasing some of its own shares in the market, and cancelling them, as an alternative to paying a dividend. Some of...
You have been hired by Morris & Son, Inc., to manage its human resource department. As a first step, you want to determine personnel needs and assigned duties in order to prevent errors and fraud in...
At its December 31 year-end, Accounts Receivable totaled $86,600, aged as follows: (1) 130 days old, $71,000; (2) 3190 days old, $12,000; and (3) more than 90 days old, $3,600. Experience has shown...
Use any method to evaluate the limit or show that it does not exist. lim (x,y)(0,0) x - y x + y
(S, T) is seawater density (kilograms per cubic meter) as a function of salinity S (parts per thousand) and temperature T (degrees Celsius). Refer to the contour map in Figure 25. Calculate the...
Briefly describe the distinguishing characteristics of a health maintenance organization (HMO). How does an HMO differ from the other insurers operating in the health insurance field?
Case study: Sun City - improving operations performance to enhance guest experience 1. Describe how Sun City implements the five operations performance objectives or principles. 2. Using your...
What recommendations do you have to increase the likelihood of success? E.g., how would you reduce the likelihood of having to go back to A4? How would you reduce the impact of having to go back to...
Problem 4 An electrically heated, square plate (0.4mx 0.4 mx0.005 m) is suspended in air of temperature Too = 20C. Find the electrical power needed to maintain the plate at T=95C if the plate is (a)...
Number of units Unit Cost Sales Beginning inventory 800 $50 Purchased 600 $52 Sold 400 $80 Sold 350 $90 Ending inventory 650 In the table below, calculate the dollar value for the period for each of...
10. Dr. D went to MGM Springfield casino while the class was taking their midterm exam. He played a Konami machine entitled 88 Fortunes. A slot attendant accidently left the slot manual next to the...
For each function, determine whether it is one-to-one, and if the function is one-to-one, find a formula for its inverse. a. f (x) = - 2 / x b. f (x) = 3 + x2
Define a traverse in Surveying?
Evaluate the expression. 60 20
Evaluate the expression. 47 25
Evaluate the expression. 37 19
Present Value Computations Using the present value tables, solve the following. ( Click here to access the PV and FV tables to use with this problem. ) Round your answers to two decimal places....
A company provided the following data: Sales $887,000 Variable costs $546,800 Fixed costs $310,000 Expected production and sales in units 36,000 What is the break-even point in sales dollars? Please...
How to solve them..equation and explain ..please.. 1. Selected information from the companys financial records is presented below Equipment, December 31, 2013 $300,000 Equipment, December 31, 2014...

Let Using polar coordinates, prove that and that does not exist. Show that g(x, y) = cos

Question:

f(x,y) = x/(x + y) and g(x, y) = x/(x + y).

Step by Step Answer:

Converting to polar coordinates gives T...View the full answer

Calculus

Students also viewed these Mathematics questions