Question: Let (x, y) = g(u), where u = x 2 + y 2 and g(u) is differentiable. Prove that 2 (1) + ( ) =

Let ƒ(x, y) = g(u), where u = x2 + y2 and g(u) is differentiable. Prove that

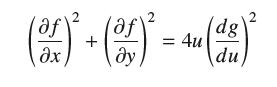
2 (1) + ( ) = 4u 2 N (dg) du

2 (1) + ( ) = 4u 2 N (dg) du

Step by Step Solution

★★★★★

3.42 Rating (171 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

Therefore af Ax 2 Si... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

Let G be the sphere x2 + y2 + z2 = a2. Evaluate each of the following: (a) (b) (c) (d) (e) Use symmetry properties to make this a trivial problem? z dS y, x + + sin z 1 + z dS x dS (r2 y) ds

Q:

A simple course management system models a student's information with a name and a set of test scores. This system should be able to create a student object with a given name and a number of scores,...

Q:

Problem 67: PIN guessing ( ) In order to get money from a cash dispenser I have to punch in a Personal Identification Number. I have forgotten my PIN, but I do know that it is equally likely to be...

Q:

My questions are in the picture how to solve for this question. Thank you very much arpChart | StockChart Question 4 - Assignment #2 (C X Lionel%20Corporation%20mar x +...

Q:

1. Let (X, x) and (Y, y) be inner product spaces over the same field F. Prove that: (a) The map : (X x Y)2 F, defined by = x + y is an F inner product on X x Y....

Q:

Mcroeconomics questions Question 1. Throughout this question we assume that all the optimization problems considered have unique solutions which are interior and characterized by the first-order...

Q:

EXAM 1 REVIEW (Actual Exam will consist of 14 problems. You may use only regular scientific calculator) 1. Knowing, that 1 + 2 + 3 + ... + n = + find 1 1+ +2+3+ ..+ 165 = 2. Knowing, that the formula...

Q:

You are designing a new syntax for a programming language like Java, with the intention of making it more approachable to students by using English words instead of punctuation symbols. (a) How does...

Q:

ACTIVITY 2 : Keep Practicing ! DERIVATIVE OF A FUNCTION AT A NUMBER Let f be a function and x = c is a value in its domain. The derivative of f with respect to x evaluated at x = c is denoted by f' (...

Q:

Jarl Company issued 8%, 8-year, $1,000,000 par value bonds that pay interest semiannually on October 1 and April 1. The bonds are dated April 1, 2014, and are issued on that date. The discount rate...

Q:

The monthly supply and demand for a particular bike is represented in the accompanying graph. The quantity is in thousands and the price is in hundreds of dollars. Use the graph to answer the...

Q:

a number of terms are provided absorption costing super - variable costing theoretical capacity practical capacity normal capacity master budget capacity non - productive idle capacity off - limits...

Q:

In evaluating marketing actions, what are the two dimensions on which they should be evaluated? AppendixLO1

Q:

Determine whether f is continuous at c. x 8 F(x) c = 2

Q:

Determine whether f is continuous at c. x + 3 f(x) c = 3

Q:

Determine whether f is continuous at c. 6 () c = -6 +6

Q:

Mary Mitchell opened a public relations firm called Music Maze on August 1, 2018. The following amounts summarize her During September 2018, the business completed the following transactions:...

Q:

In 2018 Zeus and Zilly made the following contributions to the following organizations. Charity Property Cost FMV Goodwill Clothes and misc. household items (several years old) $9,700 $2,350...

Q:

okay its a question with jus two parts but thr teo parts happen to be long! I hope you can help thisbhomeowrk due Friday at 7 am Forecast the income Statement, Balance Sheet, and Statement of Cash...