Question: Let (x, y) = x cos(y) and x = u 2 + v 2 and y = u v. af af (a) Calculate the

Let ƒ(x, y) = x cos(y) and x = u² + v²and y = u − v.

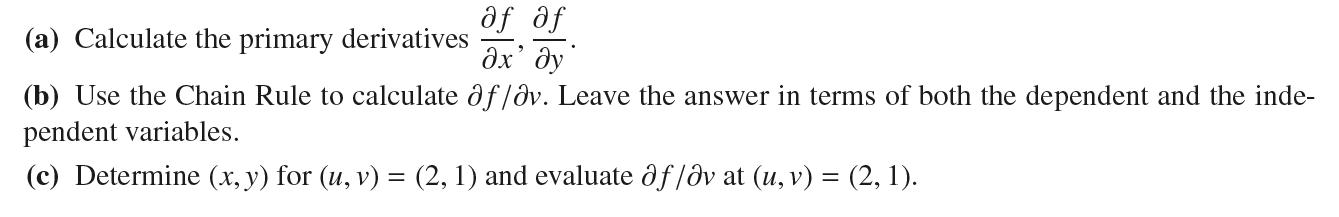
af af (a) Calculate the primary derivatives x' dy (b) Use the Chain Rule to calculate df/av. Leave the answer

af af (a) Calculate the primary derivatives x' dy (b) Use the Chain Rule to calculate df/av. Leave the answer in terms of both the dependent and the inde- pendent variables. (c) Determine (x, y) for (u, v) = (2, 1) and evaluate df/av at (u, v) = (2, 1).

Step by Step Solution

★★★★★

3.46 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The primary derivatives of fx y x cosy are af x b By ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Let U be the subspace of R3 spanned by u, = (1, 2, 3)T, u2 = (2, -1, 0)T. Let V be the subspace spanned by v1 = (5.0.3)T, v2 = (3, 1.3)T. Is V a subspace of U? Are U and V the same?

Company B had estimated 100000 direct labor hours 400000 manufacturing overhead and 25000 machine hours The actual were 100700 direct labor hours 26600 machine hours and 475000 manufacturing overhead...

p?attempt-272919&cmid=247080 0 of stion Amazon.com, suggests products you might enjoy, based on your past browsing and purchasing habits; this is an example of O a. personalization O b. customization...

1. 6 If f(z) = (5;1:2 + 6) , find the following. You do not need to simplify your answers. fla) = \\ \fGiven that f(z) = zh(z) h(-1) =2 h(-1)=5 Calculate f'(1). ' Hint: Use the product rule and the...

HW Score: 0%, O of 9 points 0 Points: 0 of1 Question 1, 16.7.5 Let S = {05 u 51, 0 Svs i} be a unit square in the Liv-plane. Find the image of S in the xy-plane under the following transformation. V...

solve these problems A binary communication channel transmits a sequence of "bits" (0s and 1s). Suppose that for any particular bit transmitted, there is a 10% chance of a transmission error (a 0...

CAS EC 505 Mathematics for Economics Assignment 4 . Let F': R?>> R be the implicit expression: F(z) = 23 + 2229 222 1029 = 0. (a) Verify that the curve traced by F (z) passes through the point z =...

Problem 07-08 Algo (Assessing the Fit of the Simple Linear Regression Model) Question 2 of 5 Check My Work (2 remaining) Click on the datafile logo to reference the data. A-Z The Toyota Camry is one...

Next question Find the derivative of y with respect to x. y = In(10x) + 9x dy dxNext question Use logarithmic differentiation to find the derivative of y with respect to t. V11t y = t . . . dy its dt...

854 CHAPTER 15 DIFFERENTIATION IN SEVERAL VARIABLES 9. 20. Jessica and I at 2 oh ; h (x , y ) = -, x = 1/2, y = 1712 paths that make a with velocity va 10. "J : f ( x , y , Z ) = xy - 22, x = rcos0,...

Which of the following has steps of the accounting cycle in proper sequence (some steps may be missing)? a. prepare a trial balance, analyze adjustment data, prepare adjusting entries, prepare...

How is the predetermined overhead rate used to allocate overhead?

Several hundred laboratory tests are performed at a large hospital each day. The rate at which these tests are done improperly (and therefore need to be redone) seems steady, at about 4%. In an...

=+18-15 How can capital budgeting tools assist in evaluating a manager who is responsible for retaining customers of a mobile telephone company?

Write a complex number in rectangular form. 4 cos + i sin 4

Write a complex number in rectangular form. 5 5 2 cos + i sin 6.

Write a complex number in rectangular form. + i sin 2 3 cos cos

List the five key principles of lean; then discuss how one of these can be used in accounting. Discuss the key benefits of adopting a lean auditing approach

Examples of mental accounting bias most likely include: Select one A. An investor who buys shares in the company for whom she works. OB. An investor holding onto an equity security until its price...

For the next fiscal year, you forecast net income of $48,100 and ending assets of $508,400. Your firm's payout ratio is 10.8%. Your beginning stockholders' equity is $296,200, and your beginning...